2021-2022学年安徽省安庆市宿松县高一（下）期中数学试卷

一、单选题（本大题共8小题，共40.0分.在每小题列出的选项中，选出符合题目的一项）

• 1．已知i为虚数单位，复数

  z

  =

  i

  -

  3

  1

  +

  i

  ，则复数

  z

  在复平面上的对应点位于（　　）

  A．第四象限

  B．第三象限

  C．第二象限

  D．第一象限
  组卷：16引用：3难度：0.8

  解析

• 2．△ABC的内角A，B，C所对的边分别为a,b,c.已知absinC=20sinB，a²+c²=41，且8cosB=1，则b=（　　）

  A．6

  B． 4 2

  C． 3 5

  D．7
  组卷：318引用：4难度：0.9

  解析

• 3．已知数列{a_n}中，a₁=2，点列P_n（n=1，2…）在△ABC内部，且△P_nAB与△P_nAC的面积比为2：1，若对n∈N^*都存在数列{b_n}满足b_n

  P

  n

  A

  +

  1

  2

  a_n+1

  P

  n

  B

  +（3a_n+2）

  P

  n

  C

  =

  0

  ，则a₃的值为（　　）

  A．26

  B．28

  C．30

  D．32
  组卷：38引用：4难度：0.6

  解析

• 4．四棱台的两底面分别是边长为x和y的正方形，各侧棱长都相等，高为z,且侧面积等于两底面积之和，则下列关系式中正确的是（　　）

  A． 1 x = 1 y + 1 z

  B． 1 y = 1 x + 1 z

  C． 1 z = 1 x + 1 y

  D． 1 z = 1 x + y
  组卷：44引用：2难度：0.7

  解析

• 5．已知双曲线

  x

  2

  9

  -

  y

  2

  b

  2

  =1（b＞0）的左顶点为A，虚轴长为8，右焦点为F，且⊙F与双曲线的渐近线相切，若过点A作⊙F的两条切线，切点分别为M，N，则|MN|=（　　）

  A．8

  B．4 2

  C．2 3

  D．4 3
  组卷：205引用：6难度：0.7

  解析

• 6．下列结论正确的选项为（　　）

  A．三棱锥的四个面都可以是直角三角形

  B．有两个面互相平行，其余各面都是平行四边形的几何体是棱柱

  C．直角三角形绕斜边所在直线旋转一周所形成的几何体是圆锥

  D．圆台的上、下底面的圆周上各取一点，则这两点的连线是圆台的母线
  组卷：28引用：3难度：0.7

  解析

• 7．在△ABC中，∠BAC=90°，2

  AD

  =

  AB

  +

  AC

  ，|

  AD

  |=|

  AB

  |=1，与

  BC

  方向相同的单位向量为

  e

  ，则向量

  AB

  在

  BC

  上的投影向量为（　　）

  A． 1 2 e

  B． - 1 2 e

  C． 3 2 e

  D． - 3 2 e
  组卷：98引用：3难度：0.6

  解析

四、解答题（本大题共5小题，共70.0分.解答应写出文字说明，证明过程或演算步骤）

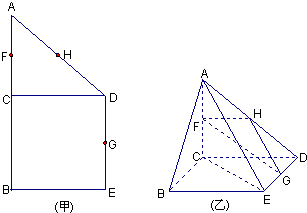• 20．如图（甲），在直角梯形ABED中，AB∥DE，AB⊥BE，AB⊥CD，且BC=CD，AB=2，F、H、G分别为AC，AD，DE的中点，现将△ACD沿CD折起，使平面ACD⊥平面CBED，如图（乙）．
  （1）求证：平面FHG∥平面ABE；
  （2）记BC=x,V（x）表示三棱锥B-ACE的体积，求V（x）的最大值；
  （3）当V（x）取得最大值时，求二面角D-AB-C的余弦值．P_n（x_n，y_n）
  组卷：136引用：5难度：0.1

  解析

• 21．某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层，每层2000平方米的楼房．经测算，如果将楼房建为x（x≥10）层，则每平方米的平均建筑费用为560+48x（单位：元）．
  （1）写出楼房平均综合费用y关于建造层数x的函数关系式；
  （2）该楼房应建造多少层时，可使楼房每平方米的平均综合费用最少？最少值是多少？
  （注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=

  购地总费用

  建筑总面积

  ）
  组卷：143引用：13难度：0.5

  解析