2023-2024学年云南省昆明十二中八年级（上）期中数学试卷
发布：2024/9/26 3:0:2
一.选择题（本大题共12个小题，每个小题只有一个正确选项，每小题3分，共36分）
-
1．“致中和，天地位焉，万物育焉．”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光．下列大学的校徽图案是轴对称图形的是（ ）
组卷：826引用：27难度：0.9 -
2．下列每组数分别表示3根小木棒的长度（单位：cm），其中能搭成一个三角形的是（ ）
组卷：880引用：17难度：0.7 -
3．如图，∠ACD是△ABC的外角，若∠ACD=105°，∠B=50°，则∠A=（ ）组卷：26引用：3难度：0.7 -
4．△ABC中，如图选项正确画出AC边上的高的图形是（ ）
组卷：902引用：8难度：0.5 -
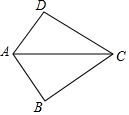5．如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）组卷：4577引用：128难度：0.7 -
6．如图．∠A+∠B+∠C+∠D+∠E的度数为（ ）组卷：1772引用：8难度：0.6 -
7．如图，△ABC≌△ADE，若∠B=80°，∠DAE=70°，则∠E的度数为（ ）组卷：416引用：10难度：0.5 -
8．已知等腰△ABC的一边长为4，周长为16，则腰长为（ ）
组卷：428引用：6难度：0.6
三.解答题（本大题共8小题，共56分）
-
23．如图①，在Rt△ABC中，∠C=90°，BC=9cm,AC=12cm,AB=15cm,现有一动点P从点A出发，沿着三角形的边AB→BC运动，到点C停止，速度为3cm/s,设运动时间为t.
（1）如图①，当t=时，△APC的面积等于△ABC面积的一半；
（2）如图②，在△DEF中，∠E=90°，DE=4cm,DF=5cm,∠D=∠A．在△ABC的边上，若另外有一动点Q，与点P同时从点A出发，沿着边AC运动，到点C停止．在两点运动过程中的某一时刻，恰好使△APQ与△DEF全等，求点Q的运动速度．
组卷：456引用：6难度：0.6 -
24．数学活动：探究利用角的对称性构造全等三角形解决问题．利用角平分线构造“全等模型”解决问题，事半功倍．
（1）尺规作图：如图，用直尺和圆规作已知角的平分线的示意图，则说明∠CAD=∠DAB的依据是三角形全等的判定 ．
【模型构造】
（2）方法一：巧翻折，造全等，
如图①，在△ABC中，AB＜AC，AD是△ABC的角平分线，则∠B ∠C．（填“＞”、“=”或“＜”）在AC上截取AE=AB，连接DE，则△ABD≌△AED（SAS）．
方法二：构距离，造全等
如图②，在四边形ABCD中，AB∥CD，∠B=90°，∠BAD和∠CDA的平分线AE，DE交BC于点E．若BC=12cm,则点E到AD的距离是 cm.过点E作EF⊥AD，垂足为点F．则△ABE≌△AFE（AAS）．
【模型应用】
（3）如图③，在△ABC中，∠A=60°，BE，CF是△ABC的两条角平分线，且BE，CF交于点P．试猜想PE与PF之间的数量关系，并说明理由．
组卷：430引用：3难度：0.1
