2022-2023学年山西省运城实验中学九年级（上）期中数学试卷

一、选择题（本大题共10小题，每小题3分，共30分。在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）

• 1．点（2，-3）与下面哪个点都在反比例函数

  y

  =

  k

  x

  的图象上（　　）

  A．（3，-2）

  B．（-2，-3）

  C．（1，6）

  D．（2，3）
  组卷：12引用：2难度：0.7

  解析

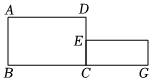• 2．如图，四边形ABCD是黄金矩形，AD＞AB，已知AD=2，则AB的长为（　　）

  A． 3 - 5

  B． 6 - 2 5

  C． 2 5 - 2

  D． 5 - 1
  组卷：26引用：2难度：0.5

  解析

• 3．函数y=kx-k与

  y

  =

  k

  x

  （

  k

  ≠

  0

  ）

  在同一坐标系中的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：322引用：25难度：0.9

  解析

• 4．已知点A（x₁，y₁），B（x₂，y₂）在反比例函数y=-

  12

  x

  的图象上．若x₁＜0＜x₂，则（　　）

  A．y1＜0＜y2

  B．y2＜0＜y1

  C．y1＜y2＜0

  D．y2＜y1＜0
  组卷：1351引用：13难度：0.6

  解析

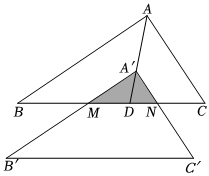• 5．如图，将△ABC沿∠BAC的平分线AD平移得到△A'B'C'的位置，A'B'交BC于点M，A'C'交BC于点N，已知△ABC的面积为81，阴影部分△A'MN的面积为16，若A'D=4，则AA'的长为（　　）

  A．5

  B．9

  C．4

  D．10
  组卷：13引用：3难度：0.5

  解析

• 6．图2是图1中长方体的三视图，若用S表示面积，S_主视图=x²+3x,S_左视图=x²+2x,则俯视图的面积为（　　）

  A．2x+10

  B．x2+6

  C．x2+5x+6

  D．x2+6x+5
  组卷：51引用：3难度：0.5

  解析

• 7．关于某个函数表达式，甲，乙，丙三位同学都正确地说出了该函数的一个特征：
  甲：函数图象经过点（-1，k²+1）；
  乙：函数的图象经过第四象限；
  丙：当x＞0时，y随x的增大而增大．
  则这个函数表达式可能是（　　）

  A．y=2x-1

  B． y = 3 x

  C．y=-2x+1

  D． y = - 3 x
  组卷：28引用：2难度：0.7

  解析

三、解答题（本大题共8个小题，共75分．解答应写出文字说明、证明过程或演算步骤）

• 22．综合与实践
  问题情境：在综合实践课上，王老师让同学们进行旋转探究，如图1，在△ABC中，AB=5，BC=7，S_△ABC=14，点D，E分别在AB，AC边上，DE∥BC，AD：BD=2：3．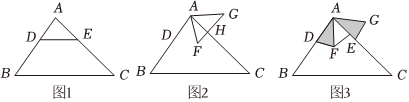
  
  问题解决
  （1）求DE的长．
  （2）如图2，将图1中的△ADE绕点A逆时针旋转得到△AFG，点D的对应点为点F，点E的对应点为点G，FG与AC交于点H，若FG⊥AC，求FH的长．
  （3）如图3，将图1中的△ADE绕点A逆时针旋转得到△AFG，点D的对应点为点F，点E的对应点为点G，连接DF，EG，若△ADF的周长为5，请你直接写出△AEG的周长为

  ．
  组卷：37引用：2难度：0.5

  解析

• 23．综合与探究
  如图，直线l：y=

  2

  3

  x-3与反比例函数y=

  k

  x

  的图象交于A，B两点，与x,y轴分别交于C，D两点，点A的纵坐标为1，点E是反比例函数y=

  k

  x

  在第一象限图象上一动点，作直线DE，交x轴于点F．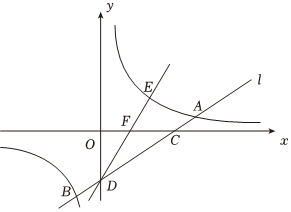
  
  （1）求k的值；
  （2）当OF：CF=2：7时，求点E的坐标；
  （3）根据图象请你直接写出不等式组

  2 3 x - 3 ＞ 0

  2 3 x - 3 ＜ k x

  的解集；
  （4）点G是x轴上一点，点P是平面内一点，在（2）的条件下，试判断是否存在这样的点P，使以A、G、E、P为顶点的四边形是矩形，若存在，请直接写出点P的坐标；若不存在，请说明理由．
  组卷：118引用：2难度：0.5

  解析