2023-2024学年江苏省宿迁市泗阳实验高级中学高二（上）第一次调研数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．经过A（-1，3），B（

  3

  ，-

  3

  ）两点的直线的倾斜角是（　　）

  A．45°

  B．60°

  C．90°

  D．120°
  组卷：408引用：5难度：0.8

  解析

• 2．圆C₁：（x+1）²+（y-3）²=36与圆C₂：（x-2）²+（y+1）²=1的位置关系是（　　）

  A．相交

  B．内切

  C．外切

  D．外离
  组卷：122引用：2难度：0.5

  解析

• 3．若点P（x,y）在直线2x+y-5=0上，O是原点，则OP的最小值为（　　）

  A． 2 2

  B．2

  C． 5

  D．4
  组卷：338引用：2难度：0.8

  解析

• 4．已知直线过点（1，2），且纵截距为横截距的两倍，则直线l的方程为（　　）

  A．2x-y=0	B．2x+y-4=0
  C．2x-y=0或x+2y-2=0	D．2x-y=0或2x+y-4=0
  组卷：966引用：28难度：0.8

  解析

• 5．圆x²+y²+4x-1=0关于点（0，0）对称的圆的标准方程为（　　）

  A．x2+y2-4x-1=0	B．x2+（y-2）2=5
  C．x2+y2+8x+15=0	D．（x-2）2+y2=5
  组卷：570引用：7难度：0.7

  解析

• 6．已知直线l₁：x+ay-a=0和直线l₂：ax-（2a-3）y-1=0，若l₁⊥l₂，则a的值为（　　）

  A．2

  B．-3

  C．0或2

  D．1或-3
  组卷：337引用：4难度：0.8

  解析

• 7．已知圆O：x²+y²=4与x轴正半轴交于点A，点B为圆上动点，点C为弦AB中点，则到直线

  x

  -

  3

  y

  +

  3

  =

  0

  的距离为

  3

  2

  的点C的个数为（　　）

  A．0

  B．1

  C．2

  D．4
  组卷：152引用：2难度：0.5

  解析

四、解答题：本大题共6小题，共计70分.解答应写出文字说明、证明过程或演算步骤.

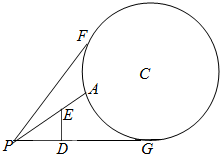• 21．如图，地面上有一竖直放置的圆形标志物，圆心为C，与地面的接触点为G．与圆形标志物在同一平面内的地面上点P处有一个观测点，且PG=50m.在观测点正前方10m处（即PD=10m）有一个高为10m（即ED=10m）的广告牌遮住了视线，因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧．
  （1）若圆形标志物半径为25m,以PG所在直线为x轴，G为坐标原点，建立直角坐标系，求圆C和直线PF的方程；
  （2）若在点P处观测该圆形标志的最大视角（即∠APF）的正切值为

  31

  49

  ，求该圆形标志物的半径．
  组卷：169引用：8难度：0.3

  解析

• 22．已知圆M的圆心在射线x+y-6=0（x≥0）上，截直线l₁：x=6所得的弦长为6，且与直线l₂：x-y+6=0相切．
  （1）求圆M的方程；
  （2）已知点N（1，1），在直线MN上是否存在点Q（异于点N），使得对圆M上的任一点P，都有

  |

  PQ

  |

  |

  PN

  |

  为定值λ？若存在，请求出点Q的坐标及λ的值；若不存在，请说明理由．
  组卷：67引用：3难度：0.6

  解析