2022-2023学年浙江省嘉兴市高二(下)期末数学试卷
发布:2024/6/15 8:0:9
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.设集合A={x|x2+x-6<0},B={x|x+1>0},则A∩B=( )
组卷:80引用:3难度:0.9 -
2.设
(i为虚数单位),则z=2+ii=( )z组卷:20引用:2难度:0.8 -
3.已知
为非零向量,且满足a,b,则b•(a+b)=0在a-b上的投影向量为( )b组卷:46引用:3难度:0.6 -
4.设函数f(x)=2|x-a|(a∈R),则“a≤0”是“f(x)在(1,+∞)上单调递增”的( )
组卷:170引用:5难度:0.5 -
5.已知α,β∈(0,π)且满足
,则( )sinα+sinβ=3(cosα+cosβ)组卷:107引用:2难度:0.6 -
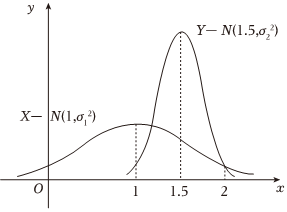 6.设.这两个正态分布密度曲线如图所示,则下列结论正确的是( )X∼N(1,σ21),Y∼N(1.5,σ22),σ1,σ2>0组卷:58引用:2难度:0.7
6.设.这两个正态分布密度曲线如图所示,则下列结论正确的是( )X∼N(1,σ21),Y∼N(1.5,σ22),σ1,σ2>0组卷:58引用:2难度:0.7 -
7.某校一场小型文艺晚会有6个节目,类型为:2个舞蹈类、2个歌唱类、1个小品类、1个相声类.现确定节目的演出顺序,要求第一个节目不排小品类,2个歌唱类节目不相邻,则不同的排法总数有( )
组卷:208引用:3难度:0.5
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
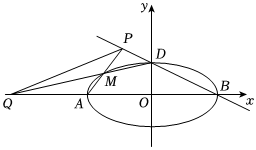 21.已知椭圆的左右顶点分别为A,B,上顶点为D,M为椭圆C上异于四个顶点的任意一点,直线AM交BD于点P,直线DM交x轴于点Q.C:x24+y2=1
21.已知椭圆的左右顶点分别为A,B,上顶点为D,M为椭圆C上异于四个顶点的任意一点,直线AM交BD于点P,直线DM交x轴于点Q.C:x24+y2=1
(1)求△MBD面积的最大值;
(2)记直线PM,PQ的斜率分别为k1,k2,求证:k1-2k2为定值.组卷:122引用:3难度:0.4 -
22.已知函数
为自然对数的底数)f(x)=alnxa-x,g(x)=ax-aex.(e=2.71828⋯
(1)当a=1时,求函数y=f(x)的最大值;
(2)已知x1,x2∈(0,+∞),且满足f(x1)>g(x2),求证:.x1+aex2>2a组卷:105引用:6难度:0.3


