当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省绍兴市诸暨市暨阳初中教育共同体九年级（上）期中数学试卷

发布：2024/8/30 6:0:10

一、选择题（本大题共10小题，每小题4分，共40分）

1．将二次函数y=（x-1）²+2的图象向上平移3个单位长度，得到的抛物线相应的函数表达式为（　　）
A．y=（x+2）²-2 B．y=（x-4）²+2 C．y=（x-1）²-1 D．y=（x-1）²+5
组卷：2370引用：18难度：0.6
解析
2．若△ABC≌△DEF，若∠A=50°，则∠D的度数是（　　）
A．50° B．60° C．70° D．80°
组卷：467引用：3难度：0.7
解析
3．从1到9这9个自然数中任取一个，是2的倍数或是3的倍数的概率是（　　）
A．
1
9
B．
2
9
C．
2
3
D．
5
9
组卷：378引用：27难度：0.7
解析
4．圆的半径为13cm,两弦：AB∥CD，AB=24cm,CD=10cm,则两弦AB、CD的距离是（　　）
A．7cm B．17cm C．12cm D．7cm或17cm
组卷：414引用：41难度：0.9
解析
5．用配方法将二次函数y=x²-8x-9化为y=a（x-h）²+k的形式为（　　）
A．y=（x-4）²+7 B．y=（x+4）²+7
C．y=（x-4）²-25 D．y=（x+4）²-25
组卷：1705引用：74难度：0.7
解析
6．已知AB=6，点P为线段AB的黄金分割点（AP＞BP），则AP的长为（　　）
A．
3
5
-
3
B．
3
5
+
3
C．
9
-
3
5
D．
9
+
3
5
组卷：49引用：3难度：0.5
解析
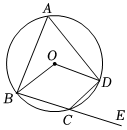7．如图，四边形ABCD内接于⊙O，点E在BC的延长线上．若∠BOD=120°，则∠DCE=（　　）
A．120° B．60° C．100° D．80°
组卷：213引用：4难度：0.7
解析
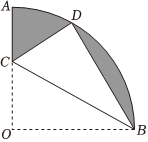8．如图，在半径为a的扇形OAB中，∠AOB=90°，将扇形OAB沿过点B的直线折叠，点O恰好落在弧AB上，折痕交OA于点C，则图中阴影部分的周长是（　　）
A．
1
2
πa
+
a
B．
1
2
πa
+
3
2
a
C．
1
2
πa
+
2
a
D．πa+2a
组卷：59引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共80分）

23．抛物线y=ax²+c与x轴交于A，B两点，顶点为C，点P为抛物线上一点，且位于x轴下方．
（1）如图1，若P（1，-3），B（4，0）．
①求该抛物线的解析式；
②若D是抛物线上一点，满足∠DPO=∠POB，求点D的坐标；
（2）如图2，已知直线PA，PB与y轴分别交于E、F两点．当点P运动时，
OE
+
OF
OC
是否为定值？若是，试求出该定值；若不是，请说明理由．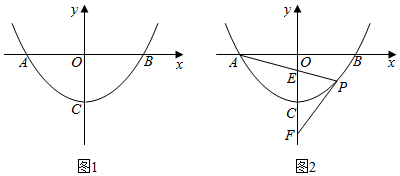
组卷：2487引用：13难度：0.3
解析
24．如图1，在平面直角坐标系中，Rt△OAB的直角边OA在y轴的正半轴上，且OA=6，斜边OB=10，点P为线段AB上一动点．

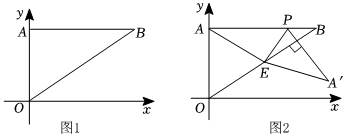
（1）请直接写出点B的坐标；
（2）若动点P满足∠POB=45°，求此时点P的坐标；
（3）如图2，若点E为线段OB的中点，连接PE，以PE为折痕，在平面内将△APE折叠，点A的对应点为A'，当PA'⊥OB时，求此时点P的坐标．
组卷：159引用：3难度：0.1
解析