2022-2023学年浙江省金华五中九年级（上）期中数学试卷

一、选择题（本题有10小题，每小题3分，共30分）

• 1．-2022的绝对值是（　　）

  A．-2022

  B．2022

  C． - 1 2022

  D． 1 2022
  组卷：670引用：147难度：0.9

  解析

• 2．下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（　　）

  A． 科克曲线	B． 笛卡尔心形线
  C． 赵爽弦图	D． 斐波那契螺旋线
  组卷：465引用：26难度：0.9

  解析

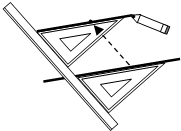• 3．如图，过直线外一点作已知直线的平行线，其依据是（　　）

  A．同旁内角互补，两直线平行

  B．内错角相等，两直线平行

  C．两点确定一条直线

  D．同位角相等，两直线平行
  组卷：109引用：4难度：0.6

  解析

• 4．一个不透明的袋中有4个白球，3个黄球和2个红球，这些球除颜色外其余都相同，则从袋中随机摸出一个球是黄球的概率为（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 1 6
  组卷：478引用：9难度：0.6

  解析

• 5．分式

  x

  +

  2

  x

  -

  3

  的值为0，则x=（　　）

  A．3

  B．-3

  C．2

  D．-2
  组卷：3引用：1难度：0.8

  解析

• 6．“儿童放学归来早，忙趁东风放纸鸢”，小明周末在龙潭公园草坪上放风筝，已知风筝拉线长100米且拉线与地面夹角为65°（如图所示，假设拉线是直的，小明身高忽略不计），则风筝离地面的高度可以表示为（　　）

  A．100sin65°

  B．100cos65°

  C．100tan65°

  D． 100 sin 65 °
  组卷：1718引用：20难度：0.7

  解析

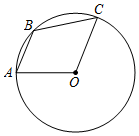• 7．如图，点A、B、C在⊙O上，AB∥OC，∠A=70°，则∠B的度数是（　　）

  A．110°

  B．125°

  C．135°

  D．165°
  组卷：438引用：5难度：0.6

  解析

• 8．已知抛物线y=x²+ax+b对称轴是直线x=1，与x轴两个交点间的距离为2，将此抛物线先向左平移2个单位，再向下平移3个单位，则所得新抛物线与x轴两个交点间的距离为（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：502引用：5难度：0.6

  解析

三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）

• 23．如图，已知抛物线y=ax²+bx-4经过A（-8，0），B（2，0）两点，直线x=-4交x轴于点C，交抛物线于点D．
  （1）求该抛物线的解析式；
  （2）点P在抛物线上，点E在直线x=-4上，若以A，O，E，P为顶点的四边形是平行四边形，求点P的坐标；
  （3）若B，D，C三点到同一条直线的距离分别是d₁，d₂，d₃，问是否存在直线l,使d₁=d₂=

  d

  3

  2

  ？若存在，请直接写出d₃的值；若不存在，请说明理由．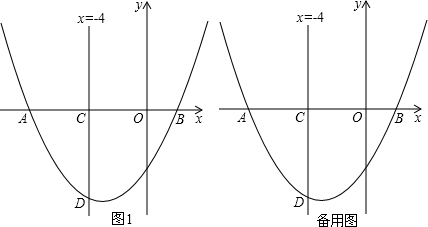
  
  组卷：802引用：54难度：0.5

  解析

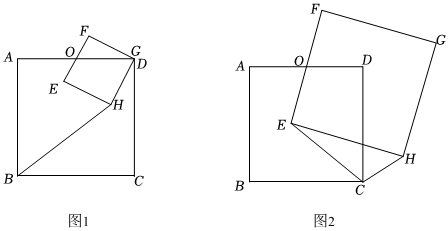• 24．如图，两个正方形ABCD与EFGH，AD与EF的中点都是O．
  （1）如图1，点D与G重合．
  ①求

  AB

  EF

  的值；
  ②连结BH，求tan∠ABH的值．
  （2）如图2，若AB=EF=6，在正方形EFGH绕点O旋转过程中，以E，C，H为顶点的三角形能否是等腰三角形？若能，求出该三角形面积；若不能，说明理由．
  组卷：28引用：2难度：0.5

  解析