2022-2023学年重庆八中高二（下）期末数学试卷

一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．若集合A={x|x²-5x-6≤0}，B={x|y=ln（2x-5）}，则（∁_RA）∩B=（　　）

  A． （ 5 2 ， 3 ]

  B． （ 5 2 ， 6 ]

  C．（3，+∞）

  D．（6，+∞）
  组卷：203引用：2难度：0.8

  解析

• 2．已知圆C：x²+y²=25，则圆C关于点（-3，4）对称的圆的方程为（　　）

  A．（x+3）2+（y-4）2=16	B．（x+3）2+（y-4）2=25
  C．（x+6）2+（y-8）2=16	D．（x+6）2+（y-8）2=25
  组卷：851引用：3难度：0.7

  解析

• 3．古代数学名著《九章算术》有如下问题：“今有女子善织，日自倍，五日织五尺，问日织几何？“意思是：一女子善于织布，每天织的布是前一天的2倍，已知她5天共织布5尺，问该女子每天分别织布多少？按此条件，若织布的总尺数不少于25尺，该女子需要的天数至少为（　　）

  A．7

  B．8

  C．9

  D．10
  组卷：58引用：1难度：0.7

  解析

• 4．已知正三棱锥的底面边长为6，高为3，则该三棱锥的表面积是（　　）

  A． 54 3

  B． 27 3

  C． 18 3

  D． 15 3
  组卷：196引用：1难度：0.8

  解析

• 5．下列说法中正确的是（　　）

  A．“A与B是对立事件”是“A与B互为互斥事件”的必要不充分条件

  B．已知随机变量X服从二项分布 B （ 4 ， 1 3 ） ，则 E （ X ） = 8 9

  C．已知随机变量X服从正态分布N（4，σ2）且P（X≤6）=0.85，则P（2＜X≤4）=0.35

  D．已知随机变量X的方差为D（X），则D（2X-3）=4D（X）-3
  组卷：40引用：1难度：0.7

  解析

• 6．设函数f（x）的定义域为R，f'（x）是其导函数，若f（x）+f'（x）＞0，f（1）=1，则不等式f（x）＞e^1-x的解集是（　　）

  A．（0，+∞）

  B．（1，+∞）

  C．（-∞，0）

  D．（0，1）
  组卷：89引用：1难度：0.5

  解析

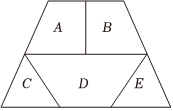• 7．用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域A，B，C，D，E涂色，要求同一区域用同一种颜色，有公共边的区域使用不同颜色，则共有（　　）种不同的涂色方法．

  A．960种

  B．840种

  C．720种

  D．120种
  组卷：93引用：1难度：0.7

  解析

四、解答题（共70分，解答应写出文字说明、证明过程成演算步骤）

• 21．已知

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的右焦点为F，A，B是椭圆上关于原点O对称的两个动点，当点A的坐标为

  （

  -

  1

  ，

  14

  2

  ）

  时，△ABF的周长恰为

  7

  2

  ．
  （1）求椭圆的方程；
  （2）过点F作直线l交椭圆于C，D两点，且CD∥AB，求△ACD面积的最大值．
  组卷：102引用：1难度：0.5

  解析

• 22．已知函数f（x）=1+lnx+kx（k∈R）．
  （1）求f（x）的单调区间；
  （2）若函数

  F

  （

  x

  ）

  =

  |

  e

  x

  -

  f

  （

  x

  ）

  x

  |

  的最小值为0，求实数k的取值范围．
  组卷：35引用：1难度：0.3

  解析