当前位置：试卷中心 > 试卷详情

2023-2024学年北京市东城区文汇中学九年级（上）期中数学试卷

发布：2024/10/3 9:0:2

一、选择题（每小题只有一个选项符合题意，每题2分，共16分）

1．抛物线y=x²+1的对称轴是（　　）
A．直线x=-1 B．直线x=1 C．直线x=0 D．直线y=1
组卷：1540引用：16难度：0.8
解析
2．下列手机手势解锁图案中，是中心对称图形的是（　　）
A． B． C． D．
组卷：2081引用：76难度：0.9
解析
3．将抛物线y=2x²平移后得到抛物线y=2x²+1，则平移方式为（　　）
A．向左平移1个单位 B．向右平移1个单位
C．向上平移1个单位 D．向下平移1个单位
组卷：155引用：17难度：0.7
解析
4．用配方法解方程x²+6x+2=0，配方正确的是（　　）
A．（x+3）²=9 B．（x-3）²=9 C．（x+3）²=6 D．（x+3）²=7
组卷：161引用：12难度：0.9
解析
5．若关于x的一元二次方程（a-1）x²+a²x-a=0有一个根是x=1，则a的值为（　　）
A．-1 B．0 C．1 D．-1或1
组卷：545引用：12难度：0.6
解析
6．平面直角坐标系中，若点A（x₁，2）和B（x₂，4）在反比例函数
y
=
k
x
（
k
＞
0
）
图象上，则下列关系式正确的是（　　）
A．x₁＞x₂＞0 B．x₂＞x₁＞0 C．x₁＜x₂＜0 D．x₂＜x₁＜0
组卷：1383引用：17难度：0.8
解析
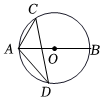7．如图，在⊙O中，AB是直径，弦AC的长为5，点D在圆上，且∠ADC=30°，则⊙O的半径为（　　）
A．2.5 B．5 C．7.5 D．10
组卷：818引用：6难度：0.6
解析
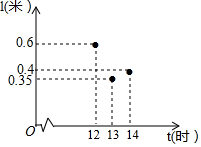8．太阳影子定位技术是通过分析视频中物体的太阳影子变化，确定视频拍摄地点的一种方法．为了确定视频拍摄地的经度，我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻．在一定条件下，直杆的太阳影子长度l（单位：米）与时刻t（单位：时）的关系满足函数关系l=at²+bt+c（a,b,c是常数），如图记录了三个时刻的数据，根据上述函数模型和记录的数据，则该地影子最短时，最接近的时刻t是（　　）
A．12.75 B．13 C．13.33 D．13.5
组卷：321引用：7难度：0.7
解析

二、填空题（本题共16分，每小题2分）

9．点A（-3，y₁），B（2，y₂）在抛物线y=-x²上，则y₁
y₂（填“＞”，“＜”或“=”）．
组卷：26引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共68分，17题6分，18题4分，19-22题每题5分，23-26题每题6分，27、28题每题7分）

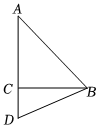27．如图，△ABC是等腰直角三角形，∠ACB=90°，AC=BC，D为AC延长线上一点，连接BD，将线段BD绕点D逆时针旋转90°得到线段DE，过点E作EF⊥AC于点F，连接AE．
（1）依题意补全图形；
（2）比较AF与CD的大小，并证明；
（3）连接BE，G为BE的中点，连接CG，用等式表示线段CD，CG，BC之间的数量关系，并证明．
组卷：1315引用：5难度：0.2
解析
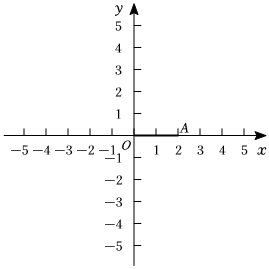28．在平面直角坐标系xOy中，给定线段AB和点P，若满足PA＜AB＜PB或者PB＜AB＜PA，则称点P为线段AB的偏序点．
（1）已知点A（2，0），
①在点B₁（-1，0），
B
2
（
1
，
3
）
，B₃（2，3），B₄（3，-1）中，是线段OA的偏序点的有
；
②若直线l：y=x+b上存在线段OA的偏序点，求b的取值的范围．
（2）已知点M（-1，0），
N
（
0
，
3
）
，⊙C是以1为半径的圆，并且圆心C在x轴上运动，若线段MN上的点均为⊙C的某条直径的偏序点，直接写出点C的横坐标c的取值的范围．
组卷：246引用：2难度：0.1
解析