当前位置：试卷中心 > 试卷详情

2022-2023学年山西省运城市盐湖区九年级（上）期中数学试卷

发布：2024/9/26 7:0:1

2．下列说法正确的是（　　）

A．某彩票的中奖概率是1%，那么买100张彩票一定有1张中奖

B．某次试验投掷图钉500次，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616

C．如果一个事件发生的可能性很小，那么它的概率为0

D．试验得到的频率与概率不可能相等

组卷：55引用：3难度：0.5

3．用配方法解方程x²+6x-7=0时，原方程应变形为（　　）
A．（x+3）²=2 B．（x+3）²=16 C．（x+6）²=2 D．（x+6）²=16
组卷：8引用：2难度：0.5
解析
4．如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（-9，0），（6，0），点D在y轴上，则点C的坐标是（　　）
A．（9，6） B．（-15，12） C．（-9，6） D．（15，12）
组卷：59引用：6难度：0.5
解析
5．下面一定相似的一组图形为（　　）
A．两个等腰三角形 B．两个矩形
C．两个等边三角形 D．两个菱形
组卷：450引用：7难度：0.5
解析
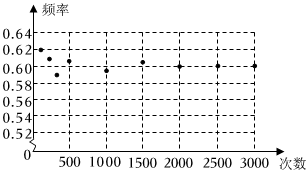6．在一个不透明的口袋中，放置4个黄球和n个蓝球，这些小球除颜色外其余均相同，课外兴趣小组每次摸出一个球记录下颜色后再放回，并且统计了蓝球出现的频率（如图所示），则n的值最可能是（　　）
A．4 B．5 C．6 D．7
组卷：38引用：1难度：0.5
解析
7．如图，在矩形ABCD中，AB=5，对角线AC与BD相交于点O，DE平分∠ODC，交AC于E，AE=3CE，则DE的长为（　　）
A．
5
2
B．4 C．
5
2
2
D．
5
2
3
组卷：30引用：1难度：0.6
解析

22．如图，在Rt△ABC中，∠B=90°，AC=30cm,∠C=30°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒．过点D作DF⊥BC于点F，连接DE，EF．
（1）四边形AEFD能构成菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
（2）当t为何值时，△DEF为直角三角形？请说明理由．
组卷：45引用：1难度：0.5
解析
23．如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论：（要求用文字语言叙述）

写出证明过程（先画出图形，写出已知、求证）．
（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．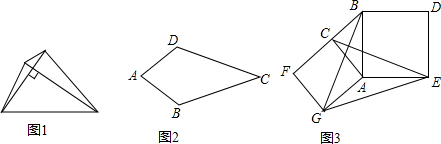
组卷：2686引用：21难度：0.1
解析