2022-2023学年河南省商丘市豫选命题联考高一(下)期末数学试卷
发布:2024/6/28 8:0:9
一、单选题。(共40分,每小题5分)
-
1.已知复数z满足
,则|z|=( )z=21-i+i组卷:298引用:13难度:0.8 -
2.在△ABC中,若AB=4,BC=5,AC=6,则
=( )AB•BC组卷:152引用:8难度:0.7 -
3.A,B两名学生均打算只去甲、乙两个城市中的一个上大学,且两人去哪个城市互不影响,若A去甲城市的概率为0.6,B去甲城市的概率为0.2,则A,B不去同一城市上大学的概率为( )
组卷:101引用:6难度:0.7 -
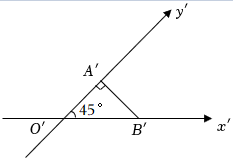 4.如图Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是( )组卷:1590引用:48难度:0.9
4.如图Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是( )组卷:1590引用:48难度:0.9 -
5.已知数据x1,x2,⋯,xn是某市n(n≥3,n∈N*)个普通职工的年收入(单位:元),若去掉一个最高年收入和一个最低年收入,则新数据与原数据相比,一定不变的数字特征是( )
组卷:109引用:5难度:0.9 -
6.在△ABC中,角A,B,C的对边分别为a,b,c,若sinA=sinBcosC且
,c=23,则A=π6=( )c+asinC+sinA组卷:271引用:5难度:0.6 -
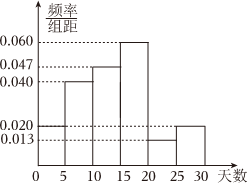 7.某游泳馆统计了2022年8月1日到30日某小区居民在该游泳馆的锻炼天数,得到如图所示的频率分布直方图(将频率视为概率),则下列说法正确的是( )组卷:38引用:2难度:0.8
7.某游泳馆统计了2022年8月1日到30日某小区居民在该游泳馆的锻炼天数,得到如图所示的频率分布直方图(将频率视为概率),则下列说法正确的是( )组卷:38引用:2难度:0.8
四、解答题。(共70分,17题10分,其余小题12分)
-
21.在△ABC中,内角A,B,C的对边分别为a,b,c,且
.bsinA+sinC=a-csinB+csinA+sinC
(1)求角A的大小;
(2)若a=2bcosB,a=3,求BC边上中线的长.组卷:259引用:3难度:0.5 -
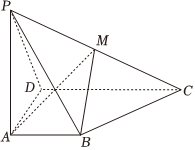 22.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥平面PAD,PA=AD=DC=2AB=4,PD=2,M是PC的中点.7
22.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥平面PAD,PA=AD=DC=2AB=4,PD=2,M是PC的中点.7
(1)证明:BM∥面PAD;
(2)证明:平面ABM⊥平面PCD;
(3)求三棱锥M-PAB的体积.组卷:305引用:4难度:0.5


