2022-2023学年江苏省连云港市赣榆区高二（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．直线x+2y+4=0在y轴上的截距为（　　）

  A．-4

  B．-2

  C．2

  D．4
  组卷：39引用：4难度：0.9

  解析

• 2．抛物线y²=16x的焦点坐标为（　　）

  A．（0，4）

  B．（0，-4）

  C．（4，0）

  D．（-4，0）
  组卷：47引用：8难度：0.9

  解析

• 3．设a为实数，若直线2x+4y-1=0与直线x+（a-1）y+2=0平行，则a的值为（　　）

  A．5

  B．3

  C．2

  D． 1 2
  组卷：6引用：1难度：0.8

  解析

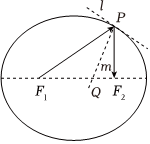• 4．班级物理社团在做光学实验时，发现了一个有趣的现象：从椭圆的一个焦点发出的光线经椭圆形的反射面反射后将汇聚到另一个焦点处．根据椭圆的光学性质解决下面问题：已知椭圆C的方程为

  x

  2

  16

  +

  y

  2

  12

  =1，其左、右焦点分别是F₁，F₂，直线l与椭圆C切于点P，且PF₁=5，过点P且与直线l垂直的直线m与椭圆长轴交于点Q，则

  F

  1

  Q

  F

  2

  Q

  =（　　）

  A． 5 2

  B． 15 3

  C． 5 4

  D． 5 3
  组卷：30引用：4难度：0.7

  解析

• 5．已知点A（2，1），点B在直线x-y+3=0上，则|AB|的最小值为（　　）

  A． 5

  B． 26

  C．2 2

  D．4
  组卷：337引用：14难度：0.8

  解析

• 6．已知圆C：x²+y²+2x-6y+6=0，P为直线1：x-2y+2=0上的动点，过点P作圆C的切线PA，PB，切点为A，B，当四边形APBC的面积最小时，直线AB的方程为（　　）

  A．x-2y-3=0

  B．x+2y-3=0

  C．x-2y+3=0

  D．x+2y+3=0
  组卷：35引用：1难度：0.5

  解析

• 7．双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的右顶点为A，点M，N均在C上，且关于y轴对称．若直线AM，AN的斜率之积为-

  5

  4

  ，则C的离心率为（　　）

  A． 3 2

  B． 3 5 5

  C． 6 2

  D． 5 2
  组卷：37引用：1难度：0.5

  解析

四、解答题：本题共6小题，共70分。请在答题卡指定区域内作答。解答时应写出文字

• 21．已知圆C：x²+y²-2x-6=0和定点A（-4，0），直线l：y=m（x+6）-8（m∈R）．
  （1）当m=1时，求直线1被圆C所截得的弦长；
  （2）若直线l上存在点M，过点M作圆C的切线，切点为B，满足MA=

  2

  MB，求m的取值范围．
  组卷：157引用：9难度：0.5

  解析

• 22．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的焦距为2

  6

  ，且椭圆经过点A（2，1）．
  （1）求椭圆C的方程；
  （2）设直线l交C于P，Q两点，直线AP，AQ的斜率之和为0，求l的斜率．
  组卷：39引用：1难度：0.5

  解析