2023年浙江省金华市金东区中考数学二模试卷

一、仔细选一选（本大题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不得分．）

• 1．实数2，0，

  -

  3

  ，-0.4中，最小的数是（　　）

  A．2

  B．0

  C． - 3

  D．-0.4
  组卷：155引用：5难度：0.6

  解析

• 2．若长度分别为a,2，3的三条线段能组成一个三角形，则a的值可能是（　　）

  A．1

  B．2

  C．5

  D．8
  组卷：318引用：1难度：0.7

  解析

• 3．金华市2022年全市地区生产总值（GDP）约为55562.47亿元，其中数55562.47用科学记数法表示为（　　）

  A．5.556247×104	B．5.556247×103
  C．55.56247×103	D．0.5556247×105
  组卷：20引用：1难度：0.8

  解析

• 4．某公园供游客休息的石板凳如图所示，它的左视图是（　　）
  ​

  A．

  B．

  C．

  D．
  组卷：266引用：5难度：0.8

  解析

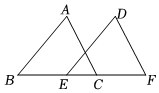• 5．如图，点B，E，C，F共线，AB∥DE，∠A=∠D，添加一个条件，不能判断△ABC≌△DEF的是（　　）

  A．AB=DE

  B．∠ACB=∠F

  C．BE=CF

  D．AC=DF
  组卷：991引用：6难度：0.6

  解析

• 6．在一个不透明的袋子里，装有3个红球、2个白球，它们除颜色外都相同，从袋中任意摸出一个球为红球的概率是（　　）

  A． 1 2

  B． 2 5

  C． 3 5

  D． 2 3
  组卷：221引用：4难度：0.8

  解析

• 7．我国在清朝时期的课本中用“”来表示代数式

  d

  2

  5

  -

  c

  2

  3

  +

  a

  2

  b

  2

  27

  ，那么“”的化简结果是（　　）

  A． 8 15 a 3 b 2

  B． 2 15 a 3 b 2

  C． 8 a 3 b 2

  D． 2 a 3 b 2
  组卷：57引用：2难度：0.8

  解析

• 8．如图，将5个大小相同的长方形置于平面直角坐标系中，若顶点A（2，9），B（6，3），则顶点C的坐标是（　　）

  A．（4，5）

  B．（3，5）

  C．（4，7）

  D．（5，6）
  组卷：250引用：7难度：0.7

  解析

三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）

• 23．定义：若n为常数，当一个函数图象上存在横、纵坐标和为n的点，则称该点为这个函数图象关于n的“恒值点”，例如：点（1，2）是函数y=2x图象关于3的“恒值点”．
  （1）判断点（1，3），（2，8），（3，7）是否为函数y=5x-2图象关于10的“恒值点”．
  （2）如图1，抛物线y=2x²+bx+2与x轴交于A，B两点（A在B的左侧），现将抛物线在x轴下方的部分沿x轴翻折，抛物线的其余部分保持不变，所得的新图象如图2所示．
  ①求翻折后A，B之间的抛物线解析式．（不必写出x的取值范围）
  ②当新图象上恰好有3个关于c的“恒值点”时，请用含b的代数式表示c.
  组卷：215引用：1难度：0.1

  解析

• 24．如图1，在矩形ABCD中，AB=4，BC=5，动点P从点C出发，以1个单位每秒速度，沿线段CD运动，同时，动点Q从点B出发，以2个单位每秒速度，沿射线BC运动，当点P到达点D时，点P，Q同时停止运动，设运动时间为t秒．
  （1）请用含t的代数式表示线段CQ的长．
  （2）如图2，AC与PQ交于点M，当BQ=5CQ时，求△PMC与△QMC的面积之比．
  （3）在点P，Q的整个运动过程中，直线AC上是否存在点E，使以PE为直角边的Rt△PQE，与以点P，Q，C三点为顶点的三角形相似？若不存在，说明理由；若存在，求t的值．
  
  组卷：121引用：1难度：0.1

  解析