2021-2022学年湖南省邵阳市新邵二中高一（下）期中数学试卷

一、解答题（共8小题，满分40分）

• 1．在复平面内，复数z=3-4i,则

  z

  对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：321引用：6难度：0.9

  解析

• 2．已知向量

  m

  =（2a,-1），

  n

  =（3，a+2），若

  m

  ⊥

  n

  ，则a=（　　）

  A．1

  B． 3 5

  C． 1 3

  D． 2 5
  组卷：226引用：5难度：0.8

  解析

• 3．△ABC的内角A，B，C的对边分别为a,b,c,且a=1，

  c

  =

  3

  ，

  B

  =

  π

  6

  ，则△ABC的面积为（　　）

  A． 3 2

  B． 3 4

  C． 3 2 或 3

  D． 3 2 或 3 4
  组卷：838引用：7难度：0.9

  解析

• 4．圆锥的母线长是4，侧面积是4π，则该圆锥的高为（　　）

  A． 15

  B．4

  C．3

  D．2
  组卷：357引用：7难度：0.7

  解析

• 5．设

  e

  1

  ，

  e

  2

  是两个不共线的向量，若向量

  m

  =

  -

  e

  1

  +

  k

  e

  2

  （

  k

  ∈

  R

  ）

  与向量

  n

  =

  e

  2

  -

  2

  e

  1

  共线，则（　　）

  A．k=0

  B．k=1

  C．k=2

  D． k = 1 2
  组卷：252引用：8难度：0.7

  解析

• 6．在△ABC中，BD=2DC．若

  AB

  =

  a

  ，

  AC

  =

  b

  ，则

  AD

  =（　　）
  

  A． 2 3 a + 1 3 b

  B． 2 3 a - 1 3 b

  C． 1 3 a + 2 3 b

  D． 1 3 a - 2 3 b
  组卷：820引用：7难度：0.9

  解析

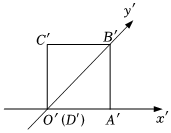• 7．如图，正方形A'B'C'D'的边长为1，它是一个水平放置的平面图形的直观图，原图形的面积为（　　）

  A． 4 2

  B． 2 2

  C． 2

  D． 2 2
  组卷：71引用：4难度：0.8

  解析

四、解答题（共6小题，满分70分）

• 21．已知a,b,c分别是△ABC内角A，B，C的对边，且满足（b-c）²=a²-bc.
  （1）求角A的大小；
  （2）若a=3，sinC=2sinB，求△ABC的面积．
  组卷：188引用：17难度：0.7

  解析

• 22．已知向量

  a

  =

  （

  3

  ，-

  1

  ）

  ，

  b

  =

  （

  1

  2

  ，

  3

  2

  ）

  ．
  （Ⅰ）求与

  a

  平行的单位向量

  c

  ；
  （Ⅱ）设

  x

  =

  a

  +

  （

  t

  2

  +

  3

  ）

  b

  ，

  y

  =

  -

  k

  •

  t

  a

  +

  b

  ，若存在t∈[0，2]使得

  x

  ⊥

  y

  成立，求k的取值范围．
  组卷：411引用：10难度：0.3

  解析