2022-2023学年安徽省安庆市桐城二中八年级（上）期中数学试卷

一、选择题（4分×10=40分）

• 1．下列函数关系中表示一次函数的有（　　）
  ①y=2x+1；②

  y

  =

  1

  x

  ；③

  y

  =

  x

  +

  1

  2

  -

  x

  ；④s=60t；⑤y=100-25x.

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：2780引用：29难度：0.9

  解析

• 2．下列选项中，可以用来说明命题“若|x|＞1，则x＞1”是假命题的反例是（　　）

  A．x=-2

  B．x=-1

  C．x=1

  D．x=2
  组卷：217引用：11难度：0.7

  解析

• 3．函数

  y

  =

  1

  -

  x

  x

  的自变量x的取值范围是（　　）

  A．x≥1且x≠0

  B．x≠0

  C．x≤1且x≠0

  D．x≤1
  组卷：2958引用：12难度：0.8

  解析

• 4．已知点A（a+1，4），B（3，2a+2），若直线AB∥x轴，则A、B间的距离是（　　）

  A．5

  B．1

  C．3

  D．0.5
  组卷：27引用：2难度：0.6

  解析

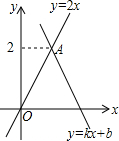• 5．如图，函数y=kx+b（k≠0）的图象经过点B（2，0），与函数y=2x的图象交于点A，则不等式0＜kx+b＜2x的解集为（　　）

  A．x＞0

  B．0＜x＜1

  C．1＜x＜2

  D．x＞2
  组卷：5247引用：22难度：0.9

  解析

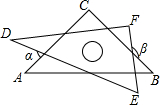• 6．小明把一副含45°，30°的直角三角板如图摆放，其中∠C=∠F=90°，∠A=45°，∠D=30°，则∠α+∠β等于（　　）

  A．180°

  B．210°

  C．360°

  D．270°
  组卷：8569引用：64难度：0.7

  解析

• 7．有下列命题：
  ①两条直线被第三条直线所截，同位角相等；
  ②0.1的算术平方根是0.01；
  ③算术平方根等于它本身的数是1；
  ④如果点P（3-2n,1）到两坐标轴的距离相等，则n=1；
  ⑤若a²=b²，则a=b；
  ⑥若

  3

  a

  =

  3

  b

  ，则a=b.
  其中假命题的个数是（　　）

  A．3个

  B．4 个

  C．5个

  D．6个
  组卷：146引用：5难度：0.9

  解析

三、解答题

• 22．某服装店同时购进甲、乙两种款式的运动服共300套，进价和售价如表中所示，设购进甲款运动服x套（x为正整数），该服装店售完全部甲、乙两款运动服获得的总利润为y元．
  （1）求y与x的函数关系式；
  （2）该服装店计划投入2万元购进这两款运动服，则至少购进多少套甲款运动服？若售完全部的甲、乙两款运动服，则服装店可获得的最大利润是多少元？
  （3）在（2）的条件下，若服装店购进甲款运动服的进价降低a元（其中20＜a＜40），且最多购进240套甲款运动服，若服装店保持这两款运动服的售价不变，请你设计出使该服装店获得最大销售利润的购进方案．
  

  运动服款式	甲款	乙款
  进价（元/套）	60	80
  售价（元/套）	100	150
  组卷：1041引用：5难度：0.5

  解析

• 23．如图1，已知∠MON=60°，A、B两点同时从点O出发，点A沿射线ON运动，点B沿射线OM运动．
  
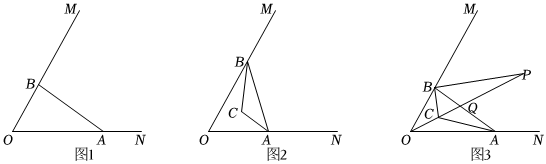
  （1）如图2，点C为△ABO三条内角平分线交点，连接BC、AC，在点A、B的运动过程中，∠ACB的度数是否发生变化？若不发生变化，求其值；若发生变化，请说明理由；
  （2）如图3，在（1）的条件下，连接OC并延长，与∠ABM的角平分线交于点P，与AB交于点Q．
  ①∠P与∠BAO的数量关系为

  ．
  ②在△BCP中，如果有一个角是另一个角的2倍，求∠BAO的度数．
  组卷：218引用：4难度：0.5

  解析