2022-2023学年山东省烟台市牟平区、开发区九年级(下)期中数学试卷(五四学制)
发布:2024/7/5 8:0:9
一、选择题:(本题共10个小题,每小题3分,满分30分。每小题都给出标号A、B、C、D的四个备选答案,其中只有一个是正确的。)
-
1.-tan60°的倒数是( )
组卷:439引用:1难度:0.7 -
2.下列垃圾分类标识的图形中,既是中心对称图形又是轴对称图形的是( )
组卷:354引用:13难度:0.9 -
3.下列各式中,计算结果等于a9的是( )
组卷:64引用:1难度:0.8 -
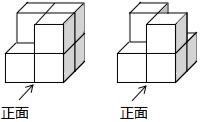 4.如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )组卷:1306引用:26难度:0.9
4.如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )组卷:1306引用:26难度:0.9 -
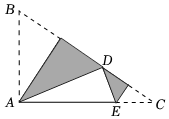 5.如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )组卷:2335引用:24难度:0.6
5.如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )组卷:2335引用:24难度:0.6 -
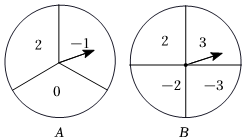 6.如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,-1;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点(x,y)落在直角坐标系y轴正半轴上的概率是( )
6.如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,-1;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点(x,y)落在直角坐标系y轴正半轴上的概率是( )
组卷:265引用:3难度:0.6 -
 7.某型号飞机的机翼形状如图所示,根据图中数据计算AB的长为( )m.组卷:1057引用:6难度:0.5
7.某型号飞机的机翼形状如图所示,根据图中数据计算AB的长为( )m.组卷:1057引用:6难度:0.5 -
8.生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2n来表示.即:21=2,22=4,23=8,24=16,25=32,…,请你推算22023的个位数字是( )
组卷:239引用:12难度:0.8
三.解答题(满分72分)
-
23.已知正方形ABCD,E为对角线AC上一点.
【建立模型】
(1)如图1,连接BE,DE.求证:BE=DE;
【模型应用】
(2)如图2,F是DE延长线上一点,FB⊥BE,EF交AB于点G.
①判断△FBG的形状并说明理由;
②若G为AB的中点,且AB=4,求AF的长.
【模型迁移】
(3)如图3,F是DE延长线上一点,FB⊥BE,EF交AB于点G,BE=BF.求证:GE=(-1)DE.2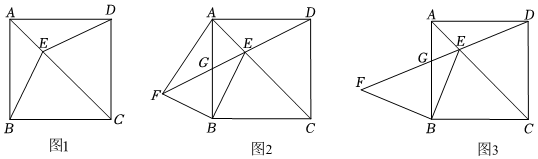 组卷:1635引用:6难度:0.2
组卷:1635引用:6难度:0.2 -
24.如图,已知抛物线:y=-2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=
,P是第一象限内抛物线上的任一点.12
(1)求抛物线的解析式;
(2)若点D为线段OC的中点,则△POD能否是等边三角形?请说明理由;
(3)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.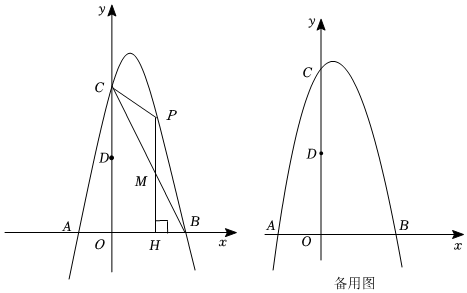 组卷:2726引用:8难度:0.3
组卷:2726引用:8难度:0.3


