2023-2024学年广东省广州三中等校联考高二(上)期中数学试卷
发布:2024/10/2 0:0:1
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.若直线l的方向向量是
,则直线l的倾斜角是( )e=(-1,3)组卷:657引用:15难度:0.8 -
2.已知方程
表示的曲线是椭圆,则实数m的取值范围是( )x22-m+y2m+1=1组卷:2309引用:7难度:0.8 -
3.若{
,a,b}为空间向量的一组基底,则下列各项中,能构成空间向量的基底的一组向量是( )c组卷:89引用:1难度:0.7 -
4.在平行六面体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=3,∠BAD=90°,∠BAA1=60°,∠DAA1=60°,则AC1的长为( )
组卷:12引用:2难度:0.7 -
5.已知过点P(1,2)的直线l,且点A(2,3)与点B(0,-5)到直线l的距离相等,则直线l的方程为( )
组卷:87引用:1难度:0.8 -
6.已知直线y=k(x+1)与曲线
两个交点,则k的取值范围为( )y=4-(x-2)2组卷:242引用:5难度:0.8 -
7.著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”事实上,很多代数问题可以转化为几何问题加以解决,如可以
转化为平面上点(x,y)与点N(a,b)的距离.结合上述观点,下列说法正确的是( )(x-a)2+(y-b)2组卷:31引用:1难度:0.8
四、解答题:本大题共6小题,满分70分,解答应写出必要的文字说明,证明过程或推演步骤。
-
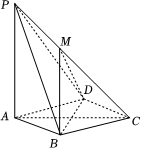 21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,∠BAD=60°.
21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,∠BAD=60°.
(1)求证:直线BD⊥平面PAC;
(2)设点M在线段PC上,且二面角C-MB-A的余弦值为,求点M到底面ABCD的距离.57组卷:54引用:3难度:0.3 -
 22.已知椭圆C:过点Ex2a2+y2b2=1(a>b>0),A1,A2为椭圆的左、右顶点,且直线A1E,A2E的斜率的乘积为(1,233).-23
22.已知椭圆C:过点Ex2a2+y2b2=1(a>b>0),A1,A2为椭圆的左、右顶点,且直线A1E,A2E的斜率的乘积为(1,233).-23
(1)求椭圆C的方程;
(2)过右焦点F的直线l与椭圆C交于M,N两点,直线l的垂直平分线交直线l于点P,交直线x=-2于点Q,求的最小值.|PQ||MN|组卷:305引用:6难度:0.4


