2020-2021学年湖南省长沙市长沙县百熙实验学校九年级（上）期中数学试卷

一、选择题（本大题共12小题，共36分）

• 1．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：13引用：1难度：0.8

  解析

• 2．在平面直角坐标系中，点A（-2，1）关于原点的对称点为A'，则点A'的坐标是（　　）

  A．（ 2，-1）

  B．（ 2，1 ）

  C．（-1，2 ）

  D．（-2，-1 ）
  组卷：73引用：3难度：0.9

  解析

• 3．若方程（m-1）x^m2+1-（m+1）x-2=0是关于x的一元二次方程，则m的值为（　　）

  A．0

  B．±1

  C．1

  D．-1
  组卷：3168引用：17难度：0.9

  解析

• 4．用配方法解方程x²-8x-20=0，下列变形正确的是（　　）

  A．（x+4）2=24

  B．（x+8）2=44

  C．（x+4）2=36

  D．（x-4）2=36
  组卷：520引用：6难度：0.6

  解析

• 5．抛物线y=2（x-3）²+4顶点坐标是（　　）

  A．（3，4）

  B．（-3，4）

  C．（3，-4）

  D．（2，4）
  组卷：4462引用：54难度：0.7

  解析

• 6．函数y=-x²+1的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：4827引用：46难度：0.7

  解析

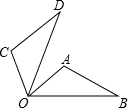• 7．如图，将△OAB绕点O逆时针旋转70°到△OCD的位置，若∠AOB=40°，则∠AOD=（　　）

  A．45°

  B．40°

  C．35°

  D．30°
  组卷：2278引用：34难度：0.6

  解析

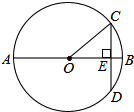• 8．如图，AB是⊙O的直径，弦CD⊥AB于点E，AB=20cm,CD=12cm,则BE=（　　）

  A．6cm

  B．5cm

  C．3cm

  D．2cm
  组卷：184引用：3难度：0.7

  解析

三、解答题（本大题共8个小题，共66分）

• 25．定义：如果二次函数y=a₁x²+b₁x+c₁（a₁≠0，a₁、b₁、c₁是常数）与y=a₂x²+b₂x+c₂（a₂≠0，a₂、b₂、c₂是常数）满足a₁+a₂=0，b₁=b₂，c₁+c₂=0，则这两个函数互为“旋转函数”．请解决下列问题：
  （1）求出二次函数y=x²-2x+1的旋转函数的顶点坐标；
  （2）若二次函数y₁=x²+（m+8n）x+16与y₂=-x²-6x+2n-7m互为“旋转函数”，直线l与函数y₁，y₂的图象都只有一个公共点，求（m+n）²⁰²⁰的值以及直线l的解析式；
  （3）在平面直角坐标系中，坐标原点为O，已知点P（2，0），⊙p与y轴相切，交x轴正半轴于点A，点B在⊙p上，且∠BAO=30°，△A′OB'与△AOB关于原点对称，若两个二次函数的图象分别经过A′、O、B′与A、O、B三点，求证：这两个二次函数互为“旋转函数”．
  组卷：505引用：2难度：0.4

  解析

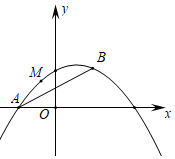• 26．如图，已知抛物线y=ax²+bx+1经过A（-1，0），B（1，1）两点．
  （1）求该抛物线的解析式；
  （2）阅读理解：
  在同一平面直角坐标系中，直线l₁：y=k₁x+b₁（k₁，b₁为常数，且k₁≠0），直线l₂：y=k₂x+b₂（k₂，b₂为常数，且k₂≠0），若l₁⊥l₂，则k₁•k₂=-1．
  解决问题：
  ①若直线y=3x-1与直线y=mx+2互相垂直，求m的值；
  ②抛物线上是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由；
  （3）M是抛物线上一动点，且在直线AB的上方（不与A，B重合），求点M到直线AB的距离的最大值．
  组卷：1507引用：5难度：0.5

  解析