当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省泰州市泰兴市九年级（上）期末数学试卷

发布：2024/7/26 8:0:9

一、选择题（本大题共有6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

1．下列方程中，是一元二次方程的是（　　）
A．2x+y=1 B．x²+3xy=6 C．x+
1
x
=4 D．x²=3x-2
组卷：1093引用：15难度：0.7
解析
2．若2x=5y,则下列式子中错误的是（　　）
A．
y
x
=
5
2
B．
y
x
=
2
5
C．
x
+
y
x
=
7
5
D．
x
-
y
y
=
3
2
组卷：557引用：6难度：0.9
解析
3．在Rt△ABC中，各边都扩大5倍，则锐角A的正切函数值（　　）
A．不变 B．扩大5倍 C．缩小
1
5
D．不能确定
组卷：1709引用：15难度：0.7
解析
4．已知一组数据a、b、c、d的平均数是3，在这组数据后再添加数据3得到一组新数据a、b、c、d、3，则新数据与原数据相比，方差将（　　）
A．不变 B．变大 C．变小 D．不能确定
组卷：451引用：3难度：0.7
解析
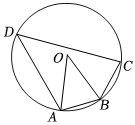5．如图，四边形ABCD内接于⊙O，AB=BC，∠BAO=75°，则∠D=（　　）
A．60° B．30° C．45° D．无法确定
组卷：646引用：4难度：0.8
解析
6．已知二次函数y=-x²+2mx,对于其图象和性质，下列说法错误的是（　　）
A．图象开口向下
B．图象经过原点
C．当x＞m时，y随x的增大而增大
D．当x＜m时，y随x的增大而增大
组卷：290引用：3难度：0.6
解析

二、填空题（本大题共有10小题，每小题3分，共30分．请把答案直接填写在答题卡相应位置上）

7．方程x²=2x的解是
．
组卷：1313引用：198难度：0.7
解析
8．大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为8cm,那么AP的长度为
cm.
组卷：873引用：21难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共有10题，共102分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

25．数学兴趣小组在探究圆中图形的性质时，用到了半径是6的若干圆形纸片．

（1）如图1，一张圆形纸片，圆心为O，圆上有一点A，折叠圆形纸片使得A点落在圆心O上，折痕交⊙O于B、C两点，求∠BAC的度数．
（2）把一张圆形纸片对折再对折后得到如图扇形，点M是弧PQ上一动点．
①如图2，当点M是弧PQ中点时，在线段OP、OQ上各找一点E、F，使得△EFM是等边三角形．试用尺规作出△EFM，不证明，但简要说明作法，保留作图痕迹．
②在①的条件下，取△EFM的内心N，则ON=
．
③如图3，当M在弧PQ上三等分点S、T之间（包括S、T两点）运动时，经过兴趣小组探究都可以作出一个△EFM是等边三角形，取△EFM的内心N，请问ON的长度是否变化．如变化，请说明理由；如不变，请求出ON的长度．
组卷：350引用：2难度：0.4
解析
26．阅读材料：小明同学在平面直角坐标系中研究中点时，发现了一个有趣的结论：若P（x₁，y₁），Q（x₂，y₂）是平面直角坐标系内两点，R（x₀，y₀）是PQ的中点，则有结论x₀=
x
1
+
x
2
2
，y₀=
y
1
+
y
2
2
．
这其实就是中点坐标公式，有了这个公式可以解决很多坐标系中求中点坐标的问题．
已知：二次函数y=x²的函数图象上分别有A，B两点，其中B（2，4），A，B分别在对称轴的异侧，C是AB中点，D是BC中点．利用阅读材料解决如下问题：
概念理解：（1）如图1，若A（-1，1），求出C，D的坐标．
解决问题：（2）如图2，点A是B关于y轴的对称点，作DE∥y轴交抛物线于点E．延长DE至F，使得DE=3EF．试判断F是否在x轴上，并说明理由．
拓展探究：（3）如图3，A（m,n）是一个动点，作DE∥y轴交抛物线于点E．延长DE至F，使得DE=3EF．
①令F（a,b），试探究b-4a值是否为定值，若是，求出这个定值；若不是，请说明理由．
②在①条件下，y轴上一点G（0，2），抛物线上任意一点H，连接GH，HF，直接写出GH+HF的最小值．
组卷：597引用：1难度：0.4
解析