2022-2023学年湖南省湘潭一中等联考高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是㣔题目要求的.

• 1．已知集合

  A

  =

  {

  x

  |

  2

  x

  ＜

  1

  }

  ，则∁_RA=（　　）

  A．（-∞，2]	B．[0，2]
  C．（2，+∞）	D．（-∞，0）∪（2，+∞）
  组卷：27引用：1难度：0.7

  解析

• 2．

  6

  -

  i

  1

  +

  i

  =（　　）

  A． 5 2 - 7 2 i

  B． 5 2 + 7 2 i

  C． 7 2 - 7 2 i

  D． 7 2 + 7 2 i
  组卷：10引用：3难度：0.8

  解析

• 3．已知函数

  f

  （

  x

  ）

  =

  a

  +

  2

  3

  x

  -

  1

  是奇函数，则f（2）=（　　）

  A． 5 4

  B．1

  C． 9 8

  D．2
  组卷：278引用：3难度：0.7

  解析

• 4．开普勒第一定律也称椭圆定律、轨道定律，其内容如下：每一行星沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点上．将某行星H看作一个质点，H绕太阳的运动轨迹近似成曲线

  x

  2

  m

  +

  y

  2

  n

  =1（m＞n＞0），行星H在运动过程中距离太阳最近的距离称为近日点距离，距离太阳最远的距离称为远日点距离．若行星H的近日点距离和远日点距离之和是18（距离单位：亿千米），近日点距离和远日点距离之积是16，则m+n=（　　）

  A．39

  B．52

  C．86

  D．97
  组卷：63引用：4难度：0.7

  解析

• 5．已知函数

  f

  （

  x

  ）

  =

  a

  x

  2

  +

  2

  x

  在（1，+∞）上不单调，则实数a的取值范围是（　　）

  A．（-∞，1）

  B．（0，1）

  C．（1，+∞）

  D． （ 0 ， 1 2 ）
  组卷：47引用：1难度：0.7

  解析

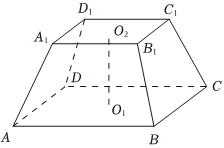• 6．如图，在四棱台ABCD-A₁B₁C₁D₁中，正方形ABCD和A₁B₁C₁D₁的中心分别为O₁和O₂，O₁O₂⊥平面ABCD，O₁O₂=3，AB=5，A₁B₁=4，则直线O₁O₂与直线AA₁所成角的正切值为（　　）

  A． 2 3

  B． 2 6

  C． 3 6

  D． 6 6
  组卷：123引用：4难度：0.8

  解析

• 7．已知函数f（x）=2sin²ωx+

  3

  sin2ωx（ω＞0）在[0，

  π

  2

  ]上恰有2个零点，则ω的取值范围是（　　）

  A．[ 7 6 ， 13 6 ）

  B．[ 4 3 ，2）

  C．[ 13 6 ， 19 6 ）

  D．[2， 10 3 ）
  组卷：80引用：4难度：0.8

  解析

四、解答题：本题共6小题，共70分.解答应写出出字说明、证明过程或演算步骤.

• 21．已知抛物线C：y²=2px（p＞0）上一点M（1，m）（m＞0）与焦点的距离为2．
  （1）求p和m；
  （2）若在抛物线C上存在点A，B，使得MA⊥MB，设AB的中点为D，且D到抛物线C的准线的距离为

  15

  2

  ，求点D的坐标．
  组卷：132引用：6难度：0.4

  解析

• 22．已知函数f（x）=3e^x-aln（x+1）．
  （1）若f（x）是增函数，求a的取值范围；
  （2）若f（x）-sinx≥3在[0，+∞）上恒成立，求a的取值范围．
  组卷：67引用：2难度：0.5

  解析