当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省南京市秦淮区七年级（下）期末数学试卷

发布：2024/6/8 8:0:9

一、选择题（本大题共8小题，每小题2分，共16分.在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卷相应位置上）

1．下列计算正确的是（　　）
A．m³•m³=2m³ B．m²+m³=m⁵ C．（m³）²=m⁶ D．m⁶÷m²=m³
组卷：167引用：2难度：0.7
解析
2．不等式2x≥-2的解集在数轴上表示正确的是（　　）
A． B．
C． D．
组卷：429引用：7难度：0.7
解析
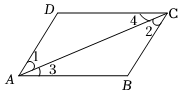3．如图，下列条件：
①∠1=∠2；
②∠3=∠4；
③∠ADC=∠B；
④∠D+∠BCD=180°；
⑤∠B+∠BCD=180°，
其中能推导出AB∥CD的是（　　）
A．①④ B．②④ C．①⑤ D．②⑤
组卷：311引用：1难度：0.5
解析
4．一个正多边形每个内角与它相邻外角的度数比为2：1，则这个正多边形是（　　）
A．正五方形 B．正六边形 C．正七边形 D．正八边形
组卷：702引用：7难度：0.8
解析
5．若多项式4a²-2ka+9可以写成一个整式的平方，则常数k的值为（　　）
A．12 B．±12 C．6 D．±6
组卷：506引用：2难度：0.9
解析
6．下列长度的三条线段与长度为5的线段能组成四边形的是（　　）
A．2，2，2 B．1，1，8 C．1，2，2 D．1，1，1
组卷：588引用：7难度：0.7
解析
7．我国古代数学名著《张丘建算经》中记载：“今有甲、乙怀钱，各不知其数，甲得乙十钱多乙余钱五倍，乙得甲十钱适等，问甲、乙怀钱各几何？”译文为：现有甲、乙两人带有一些银子，都不知道数量，甲得到乙的10两银子，甲比乙多出的银子是乙的5倍，乙得到甲的10两银子，两人的银子恰好相等，问甲、乙各带了多少两银子？设甲带了x两银子，乙带了y两银子，那么可列方程组为（　　）
A．
x
+
10
-
（
y
-
10
）
=
5
（
y
-
10
）
x
-
10
=
y
+
10
B．
x
+
10
=
5
（
y
-
10
）
x
-
10
=
y
+
10
C．
x
+
10
-
（
y
-
10
）
=
5
（
y
-
10
）
x
+
10
=
y
-
10
D．
x
-
10
=
5
（
y
+
10
）
x
-
10
=
y
+
10
组卷：637引用：9难度：0.7
解析
8．如图，C是AB上一点，分别以AC、BC为边画正方形ACDE与正方形BCFG，连接CG、DG．已知
AB
=
9
2
，△CDG的面积为
7
4
，则正方形ACDE与正方形BCFG的面积的和为（　　）
A．
67
4
B．
53
4
C．22 D．13
组卷：618引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共64分）

25．在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．
（1）如图①，当点M在线段AC上，且∠C=50°时，求证BD∥MF；
（2）当点M在边AC的延长线上时，补全图②，判断BD与MF的位置关系并证明．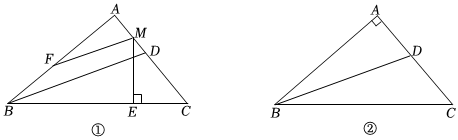
组卷：754引用：2难度：0.3
解析

26．如图，是某道路停车泊位收费公示牌．现从该收费公示牌中摘录其收费标准，并注解如图表．

一级支路计时时段/车型白天时段夜间时段

小型车连续停放6小时封顶连续停放6小时封顶

首小时内（15-60分钟）首小时后（60分钟后） 20：00至次日8：00

2元/15分钟 2元/15分钟 1元/小时

大型车 2.5元/15分钟 3元/15分钟 1.5元/小时

注解 1．白天时段，车辆进入停车泊位15分钟以内免费，第15分钟开始收费．以小型车为例，记小型车连续停放时间为a分钟，当0≤a＜15时不收费，当a=15时收费2元，当15＜a≤30时收费4元，当30＜a≤45时收费6元，当45＜a≤60时收费8元，当60＜a≤75时收费10元，以此类推．
2．夜间时段，不足1小时按1小时收费．
3．“连续停放6小时封顶”是指当车辆连续停放的时间超过6小时时，只收6小时的停车费．

【初步理解】
（1）夜间时段，一辆小型车在该道路停车泊位连续停放8小时，需缴费
元；
（2）白天时段，一辆大型车在该道路停车泊位连续停放1小时36分钟，需缴费
元；
【综合应用】
（3）白天时段，一辆小型车在该道路停车泊位连续停放一段时间后缴费26元，则该车最多停放了多长时间？（用一元一次不等式解决问题）
【深入探索】
（4）已知一辆小型车与一辆大型车在该道路停车泊位都连续停放5小时，小型车在白天时段停放m分钟，大型车在白天时段停放n分钟，且n＜60．当小型车的停车费高于大型车的停车费时，m随n的变化而变化，请直接写出n的范围及其相应的m的范围．

组卷：570引用：2难度：0.5

解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

一级支路计时	时段/车型	白天时段		夜间时段
	小型车	连续停放6小时封顶		连续停放6小时封顶
		首小时内（15-60分钟）	首小时后（60分钟后）	20：00至次日8：00
		2元/15分钟	2元/15分钟	1元/小时
	大型车	2.5元/15分钟	3元/15分钟	1.5元/小时
注解	1．白天时段，车辆进入停车泊位15分钟以内免费，第15分钟开始收费．以小型车为例，记小型车连续停放时间为a分钟，当0≤a＜15时不收费，当a=15时收费2元，当15＜a≤30时收费4元，当30＜a≤45时收费6元，当45＜a≤60时收费8元，当60＜a≤75时收费10元，以此类推． 2．夜间时段，不足1小时按1小时收费． 3．“连续停放6小时封顶”是指当车辆连续停放的时间超过6小时时，只收6小时的停车费．

A．	B．
C．	D．

2022-2023学年江苏省南京市秦淮区七年级（下）期末数学试卷

一、选择题（本大题共8小题，每小题2分，共16分.在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卷相应位置上）

1．下列计算正确的是（ ）

2．不等式2x≥-2的解集在数轴上表示正确的是（ ）

3．如图，下列条件：①∠1=∠2；②∠3=∠4；③∠ADC=∠B；④∠D+∠BCD=180°；⑤∠B+∠BCD=180°，其中能推导出AB∥CD的是（ ）

4．一个正多边形每个内角与它相邻外角的度数比为2：1，则这个正多边形是（ ）

5．若多项式4a2-2ka+9可以写成一个整式的平方，则常数k的值为（ ）

6．下列长度的三条线段与长度为5的线段能组成四边形的是（ ）

8．如图，C是AB上一点，分别以AC、BC为边画正方形ACDE与正方形BCFG，连接CG、DG．已知AB=92，△CDG的面积为74，则正方形ACDE与正方形BCFG的面积的和为（ ）

三、解答题（本大题共8小题，共64分）

1．下列计算正确的是（　　）

2．不等式2x≥-2的解集在数轴上表示正确的是（　　）

3．如图，下列条件：
①∠1=∠2；
②∠3=∠4；
③∠ADC=∠B；
④∠D+∠BCD=180°；
⑤∠B+∠BCD=180°，
其中能推导出AB∥CD的是（　　）

4．一个正多边形每个内角与它相邻外角的度数比为2：1，则这个正多边形是（　　）

5．若多项式4a²-2ka+9可以写成一个整式的平方，则常数k的值为（　　）

6．下列长度的三条线段与长度为5的线段能组成四边形的是（　　）

8．如图，C是AB上一点，分别以AC、BC为边画正方形ACDE与正方形BCFG，连接CG、DG．已知
AB
=
9
2
，△CDG的面积为
7
4
，则正方形ACDE与正方形BCFG的面积的和为（　　）