2023-2024学年河南省洛阳第一高级中学高三(上)段考数学试卷(10月份)
发布:2024/9/29 20:0:2
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.当
时,z100+z50+1=( )z=1-i2组卷:252引用:4难度:0.8 -
2.已知f(x)=xex+3sinx,则曲线y=f(x)在点(0,f(0))处的切线方程为( )
组卷:183引用:4难度:0.8 -
3.已知α,β为锐角,且tanα=2,
,则tan(α-β)=( )cos(α+β)=-31010组卷:170引用:4难度:0.6 -
4.已知在△ABC中,AB=3,AC=4,BC=5,动点M位于线段BC上,则
的最小值为( )MA•MB组卷:62引用:2难度:0.6 -
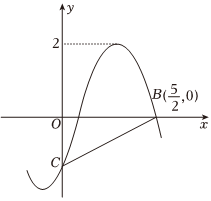 5.函数的部分图象如图所示,B,C分别为函数f(x)的图象与x轴、y轴的交点,f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2).若函数f(x)的图象与直线|BC|=332在(0,3)内的两个交点的坐标分别为(x1,y1)和(x2,y2),则f(x1+x2)=( )y=54组卷:45引用:1难度:0.7
5.函数的部分图象如图所示,B,C分别为函数f(x)的图象与x轴、y轴的交点,f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2).若函数f(x)的图象与直线|BC|=332在(0,3)内的两个交点的坐标分别为(x1,y1)和(x2,y2),则f(x1+x2)=( )y=54组卷:45引用:1难度:0.7 -
6.已知数列{an}满足a2n+1+a2n=4n-1,a2n-a2n-1=4n-3,若数列{an}的前50项和为1273,则a3=( )
组卷:84引用:1难度:0.5 -
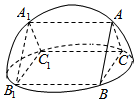 7.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )组卷:400引用:12难度:0.7
7.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )组卷:400引用:12难度:0.7
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
21.已知高三某学生为了迎接高考,参加了学校的5次模拟考试,其中5次模拟考试的成绩如表所示,
设变量x,y满足回归直线方程次数(x) 1 2 3 4 5 考试成绩(y) 498 499 497 501 505 .̂y=̂bx+̂a
(1)假如高考也符合上述的模拟考试的回归直线方程,高考看作第10次模拟考试,预测2022年的高考成绩;
(2)从上面的5次考试成绩中随机抽取3次,求其中2次成绩都大于500分的概率.
参考公式:回归直线方程中的斜率和截距的最小二乘估计公式分别为̂y=̂bx+̂a,̂b=n∑i=1(xi-x)(yi-y)n∑i=1(xi-x)2.̂a=y-̂bx组卷:196引用:6难度:0.7 -
22.已知函数f(x)=lnx+ax+x2(a∈R).
(1)函数f(x)在[1,2]上单调递增,求出实数a的取值范围;
(2)若方程f(x)=(ex+e+1)lnx在[1,+∞)上有两个不同的实根,求出实数a的取值范围.组卷:38引用:1难度:0.6


