2022-2023学年广西南宁市江南区八年级（上）期中数学试卷
发布：2024/5/28 8:0:9
一、选择题（本大题共12小题，每小题3分，共36分。每小题有四个选项，其中只有一个选项符合题意，请用2B铅笔在答题卡上将选定的选项标号涂黑。）
-
1．下列冬奥会会徽中是轴对称图形的是（ ）
组卷：297引用：9难度：0.9 -
2．下列长度的三条线段能组成三角形的是（ ）
组卷：395引用：9难度：0.8 -
3．下列四个图形中，线段BE是△ABC的高的图形是（ ）
组卷：2958引用：25难度：0.7 -
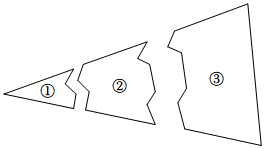4．如图，一块玻璃被打碎成三块，如果要去玻璃店配一块完全一样的玻璃，那么最合理的办法是（ ）组卷：511引用：8难度：0.7 -
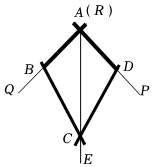5．如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A、C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是（ ）组卷：3018引用：40难度：0.7 -
6．若一个正多边形的每一个外角都等于36°，则它是（ ）
组卷：380引用：5难度：0.8 -
7．下列运算正确的是（ ）
组卷：52引用：2难度：0.5 -
8．等腰三角形的两边长分别为3和6，那么该三角形的周长为（ ）
组卷：473引用：14难度：0.9
三、简答题（本大题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤。）
-
25．如图，在△ABC中，BA=BC，D在边CB上，且DB=DA=AC．
（1）如图1，填空∠B=°，∠C=°；
（2）若M为线段BD上的点，过M作直线MH⊥AD于H，分别交直线AB、AC与点N、E，如图2
①求证：△ANE是等腰三角形；
②试写出线段BN、CE、CD之间的数量关系，并加以证明．
组卷：6196引用：16难度：0.5 -
26．综合探究：探索等腰三角形中相等的线段
问题情境：
数学活动课上，老师提出了一个问题：等腰三角形底边中点到两腰的距离相等吗？同学们就这个问题展开探究．
问题初探：
（1）希望小组的同学们根据题意画出了相应的图形，如图1．在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为点E，F．经过合作，该小组的同学得出的结论是DE=DF．并且展示了他们的证法如下：
证明：如图1，
∵DE⊥AB，DF⊥AC．
∴∠DEB=∠DFC=90°．
∵AB=AC，
∴∠B=∠C（依据1）．
∵D是BC的中点，
∴BD=CD．
在△BDE和△CDF中，，∠DEB=∠DFC∠B=∠CBD=CD
∴△BDE≌△CDF（依据2）．
∴DE=DF．
①请写出依据1和依据2的内容：
依据1：．
依据2：．
②请你应用图2写出一种不同于希望小组的证法．
问题再探：
（2）未来小组的同学经过探究又有新的发现，如果在等腰三角形ABC中，作腰AB上的高CG，如图3．则CG与DE有确定的数量关系．请你直接写出这个数量关系为．
类比探究：
（3）奋斗小组的同学认真研究过后，发现了以下两个正确结论：①在图4中，若DE，DF分别为△ABD和△ACD的中线，那么DE=DF仍然成立；②在图5中，若DE，DF分别为△ABD和△ACD的角平分线，那么DE=DF仍然成立．请你选择其中一个结论，写出证明过程．
组卷：388引用：4难度：0.2
