2022-2023学年福建省厦门外国语学校瑞景分校八年级（上）期中数学试卷

一、选择题（本愿共10小题，每小题4分，共40分.每小题只有一-个选项符合题意.）

• 1．我国重要银行的商标设计都融入了中国古代钱币的图案，下列我国四大银行的商标图案不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：57引用：12难度：0.9

  解析

• 2．在实数2，0，

  5

  ，

  π

  3

  ，

  3

  27

  ，0.1010010001…（每两个1之间依次多1个0）中，无理数的个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：66引用：5难度：0.8

  解析

• 3．现有2根木棒，它们的长分别是8cm和5cm,还需要一根木棒来组成首尾相连的三角形，应选择（　　）的木棒．

  A．2cm

  B．3cm

  C．5cm

  D．13cm
  组卷：32引用：3难度：0.7

  解析

• 4．如图，△ABC中，∠A=42°，∠B=56°，CD平分∠ACB，则∠ACD度数为（　　）

  A．82°

  B．60°

  C．45°

  D．41°
  组卷：10引用：2难度：0.7

  解析

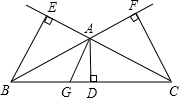• 5．如图，AD⊥BC于D，BE⊥AC于E，CF⊥AB于F，GA⊥AC于A，则△ABC中，AC边上的高为（　　）

  A．AD

  B．GA

  C．BE

  D．CF
  组卷：1108引用：9难度：0.9

  解析

• 6．已知m,n是整数，a≠0，b≠0，则下列各式中，能表示“积的乘方法则”的是（　　）

  A．anam=am+n

  B．（am）n=amn

  C．a0=1

  D．（ab）n=anbn
  组卷：326引用：6难度：0.9

  解析

• 7．如图所示的图形中，AC=AD，BC=BD，那么（　　）
  

  A．CD垂直平分AB	B．AB垂直平分CD
  C．CD平分∠ACB	D．∠CAD=∠CBD
  组卷：11引用：2难度：0.5

  解析

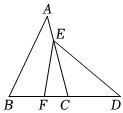• 8．如图，△ABC≌△DEF，点E在AC上，B，F，C，D四点在同一条直线上．若∠A=40°，∠CED=35°，则下列结论正确的是（　　）
  

  A．EF=EC，AB=FC	B．EF≠EC，AE=FC
  C．EF=EC，AE≠FC	D．EF≠EC，AE≠FC
  组卷：388引用：3难度：0.6

  解析

三、解答题（本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤.）

• 24．如图1，在平面直角坐标系中，点A（a,0）和点C（0，c）分别在x轴和y轴的正半轴上，并且|a-4|+（2-c）²=0．F为线段AC上一点，且满足∠FOC=∠FCO．
  
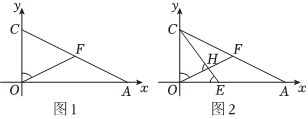
  （1）点A的坐标为

  ，点C的坐标为

  ，点F的纵坐标为

  ；
  （2）如图2，点E是线段OA上一动点（与点O、A不重合），连接CE交于点H，在点E运动过程中，探究∠OHC、∠ACE、∠OEC之间的数量关系，并证明．
  组卷：55引用：2难度：0.5

  解析

• 25．如图，△OAB是等腰直角三角形，OA=AB，点B坐标为（4，0）．C（m,0）为x轴上一点，连接AC，以点C为直角顶点在AC的左侧作等腰直角三角形ACD．
  
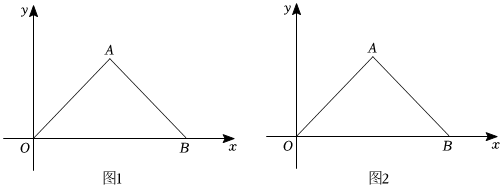
  （1）点A的坐标为

  ；
  （2）若2＜m＜4，请在图1中补全图形，并判断∠BOD是否为定值，说明理由；
  （3）如图2，当点C在x轴上移动时，∠BOD是否仍为定值，说明理由．
  组卷：13引用：1难度：0.5

  解析