2022-2023学年吉林省长春市南湖实验中学七年级（下）期末数学试卷

一、选择题：（本大题共8小题，每小题3分，共24分）

• 1．下列旗子中，不是轴对称图形的是（　　）

  A．	B．
  C．	D．
  组卷：24引用：2难度：0.7

  解析

• 2．不等式组

  2 x - 1 ≤ 3

  2 x + 3 ＞ 1

  的解集在数轴上表示正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：233引用：7难度：0.7

  解析

• 3．已知x＜y,则下列式子一定成立的是（　　）

  A．x+4＞y+4

  B．a2x＜a2y

  C．-3x＞-3y

  D． x 4 ＞ y 4
  组卷：134引用：4难度：0.7

  解析

• 4．只用下列正多边形地砖中的一种，能够铺满地面的是（　　）

  A．正十边形

  B．正八边形

  C．正六边形

  D．正五边形
  组卷：264引用：62难度：0.9

  解析

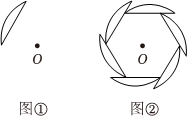• 5．利用图形的旋转可以设计出许多美丽的图案，如图②中的图案是由图①中的基本图形以点O为旋转中心，顺时针旋转5次而生成的，每一次旋转的角度均为α，则α至少为（　　）

  A．30°

  B．60°

  C．90°

  D．120°
  组卷：137引用：1难度：0.5

  解析

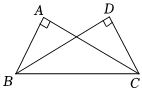• 6．如图，∠A=∠D=90°，添加下列条件中的一个后，能判定△ABC与△DCB全等的有（　　）
  ①∠ABC=∠DCB；
  ②∠ACB=∠DBC；
  ③AB=DC；
  ④AC=DB．

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：245引用：1难度：0.7

  解析

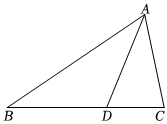• 7．如图，△ABC为锐角三角形，点D在BC边上，∠B=∠BAD=∠CAD，试作点P，使点P在AD边上，且∠APC=∠ADB，以下是甲、乙两人的作法：
  甲：分别以点A和点C为圆心，以大于

  1

  2

  AC的长为半径画弧，两弧交于点E、F，直线EF交AD于点P，则点P即为所求．
  乙：以点C为圆心，以CD长为半径画弧，交AD于点P（点P不与点D重合），则点P即为所求．
  对于甲、乙两人的作法，下列说法正确的是（　　）

  A．两人皆错误	B．两人皆正确
  C．甲正确，乙错误	D．甲错误，乙正确
  组卷：47引用：1难度：0.5

  解析

• 8．如图，将△ABC绕点A逆时针旋转43°得到△ADE，点B的对应点D恰好在BC边上，DE交AC于点F，若∠ACD=34°，则∠DFC的度数为（　　）

  A．43°

  B．77°

  C．103°

  D．113°
  组卷：251引用：2难度：0.5

  解析

三、解答题：（本大题共10小题，共78分）

• 23．【问题提出】
  如图①，在△ABC中，AB=6，AC=4，求BC边上的中线AD的取值范围．
  【问题解决】
  经过组内合作交流．小明得到了如下的解决方法：延长AD到点E，使DE=AD，连接BE，经过推理可知△ADC≌△EDB…
  （1）由已知和作图得到△ADC≌△EDB的理由是

  ．
  A．边边边
  B．边角边
  C．角边角
  D．斜边直角边
  （2）AD的取值范围为

  ．
  【方法总结】
  解题时若条件中出现“中点”或“中线”，则可以考虑将中线加倍来构造全等三角形，从而将分散的已知条件转换到同一个三角形中，我们称这种添加辅助线的方法为“倍长中线法”．
  【应用】
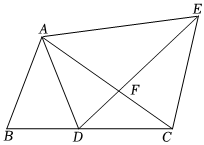
  如图②，在△ABC中，点D为BC边的中点，点E在AB边上，AD与CE相交于点F，EA=EF，求证：AB=CF．
  【拓展】
  如图，在△ABC中，∠BAC=90°，AD平分∠BAC，点E为BC边的中点，过点E作EF∥AD，交AC于点F，交BA的延长线于点G，若AF=1.5，CF=4.5，则△ABC的面积为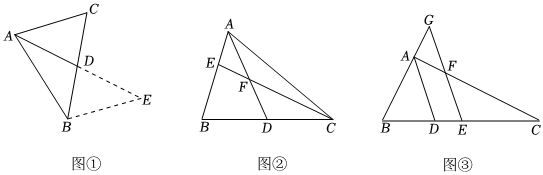

  ．
  组卷：670引用：1难度：0.5

  解析

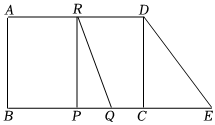• 24．如图，在长方形ABCD中，AB=CD=4，AD=BC=6，点E在BC的延长线上，CE=3，DE=5．动点P从点B出发，沿BC以每秒1个单位长度的速度向终点C运动；同时动点Q从点E出发，沿EB以每秒1.5个单位长度的速度向终点B运动．过点P作PR⊥BC交AD于点R，连接QR．设点P的运动时间为t秒．
  （1）当点P与点Q重合时，求t的值；
  （2）用含t的代数式表示线段PQ的长；
  （3）当∠PQR的大小等于∠ABC的一半时，求t的值；
  （4）当∠PQR的大小等于∠ADE的一半时，直接写出t的值．
  组卷：178引用：1难度：0.4

  解析