2022-2023学年重庆市南开中学高一（下）期末数学试卷

一、单项选择题：本题共8小题.每小题5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求.请将答案填写在答题卡相应的位置上.

• 1．直线x-

  3

  y+1=0的倾斜角为（　　）

  A．30°

  B．150°

  C．60°

  D．120°
  组卷：514引用：29难度：0.9

  解析

• 2．已知

  a

  ，

  b

  均为单位向量，且

  a

  与

  b

  夹角为60°，则

  |

  a

  -

  2

  b

  |

  =（　　）

  A．3

  B． 2

  C．2

  D． 3
  组卷：50引用：1难度：0.7

  解析

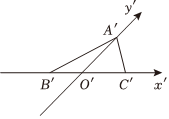• 3．将△ABC按斜二测画法得到△A′B′C′，如图所示，B′C′=2，A′B′=2，∠A′B′C′=30°，则△ABC的面积（　　）

  A．2

  B． 4 2

  C．4

  D． 2 2
  组卷：135引用：1难度：0.5

  解析

• 4．过四棱锥P-ABCD任意两条棱的中点作直线，其中与平面PBD平行的直线有（　　）

  A．4条

  B．5条

  C．6条

  D．7条
  组卷：104引用：3难度：0.8

  解析

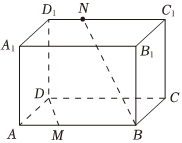• 5．如图，在长方体ABCD-A₁B₁C₁D₁中，

  AM

  =

  1

  3

  AB

  ，

  D

  1

  N

  =

  1

  3

  D

  1

  C

  1

  ，AB=3，AD=1，AA₁=2，则直线DM与BN所成角的余弦值为（　　）

  A． 3 4

  B． 2 2

  C． 1 3

  D． 2 2 3
  组卷：98引用：3难度：0.7

  解析

• 6．在△ABC中，BC边上的高

  AD

  =

  1

  2

  BC

  ，且AB≠AC，则∠A为（　　）

  A．锐角

  B．直角

  C．钝角

  D．无法确定
  组卷：26引用：1难度：0.6

  解析

• 7．已知△ABC是边长为2的正三角形，动点P满足

  CP

  =

  m

  CA

  +

  n

  CB

  ，且m+2n=1．若Q为AB的中点，则|PQ|的最小值为（　　）

  A． 1 4

  B． 1 2

  C． 3 28

  D． 21 14
  组卷：75引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.请将答案填写在答题卡相应的位置上.

• 21．在锐角△ABC中，角A，B，C所对的边分别为a,b,c,bsinA+atanAcosB=2asinC．
  （1）求A；
  （2）若D为BC延长线上一点，且

  ∠

  CAD

  =

  π

  4

  ，求

  BC

  CD

  的取值范围．
  组卷：151引用：5难度：0.5

  解析

• 22．我们把和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线．如图，在菱形ABCD中，∠BAD=60°，将△ABD沿BD翻折，使点A到点P处．E，F，G分别为BD，PD，BC的中点，且FG是PD与BC的公垂线．
  
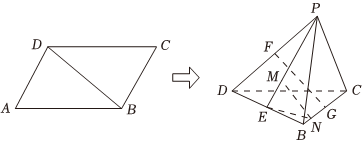
  （1）证明：三棱锥P-BCD为正四面体；
  （2）若点M，N分别在PE，BC上，且MN为PE与BC的公垂线．
  ①求

  PM

  ME

  的值；
  ②记四面体BEMN的内切球半径为r,证明：

  1

  2

  r

  ＞

  1

  EM

  +

  1

  BN

  ．
  组卷：104引用：3难度：0.5

  解析