2023-2024学年河北省保定市定州二中高二（上）月考数学试卷（10月份）

一、选择题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．若A（-2，3），B（3，-2），C（

  1

  2

  ，m）三点共线，则m的值为（　　）

  A． 1 2

  B． - 1 2

  C．-2

  D．2
  组卷：1100引用：77难度：0.9

  解析

• 2．已知向量

  a

  =（1，2，3），

  b

  =（-2，-4，-6），|

  c

  |=

  14

  ，若（

  a

  +

  b

  ）•

  c

  =7，则

  a

  与

  c

  的夹角为（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  组卷：372引用：13难度：0.7

  解析

• 3．已知

  m

  =

  （

  -

  2

  ，

  2

  ，

  5

  ）

  ，

  n

  =

  （

  3

  ，-

  2

  ，

  2

  ）

  分别是平面α，β的法向量，则平面α，β的位置关系为（　　）

  A．平行	B．垂直
  C．相交但不垂直	D．重合
  组卷：48引用：4难度：0.7

  解析

• 4．已知两点A（-1，2），B（m,3），且m∈[-

  3

  3

  -1，

  3

  -1]，则直线AB的倾斜角α的取值范围是（　　）

  A．[ π 6 ， π 2 ）	B．[ π 2 ， 2 π 3 ]
  C．[ π 6 ， π 2 ）∪（ π 2 ， 2 π 3 ]	D．[ π 6 ， 2 π 3 ]
  组卷：52引用：1难度：0.7

  解析

• 5．已知圆C：（x-2）²+y²=2，过平面上的点P引圆的两条切线l₁，l₂，使得l₁⊥l₂，则P的轨迹方程为（　　）

  A．（x-2）2+y2=16	B．（x-2）2+y2=4
  C．x2+（y-2）2=16	D．x2+（y-2）2=4
  组卷：47引用：2难度：0.6

  解析

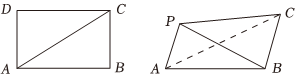• 6．已知矩形ABCD，

  AB

  =

  3

  ，AD=1，将△ACD沿AC折起到△ACP的位置若

  PB

  =

  3

  ，则二面角P-AC-B平面角的余弦值的大小为（　　）

  A． 2 2 3

  B． 1 3

  C． - 1 3

  D． - 2 2 3
  组卷：229引用：2难度：0.5

  解析

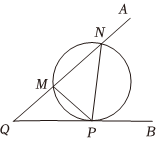• 7．几何学史上有一个著名的米勒问题：“设点M，N是锐角∠AQB的一边QA上的两点，试在边QB上找一点P，使得∠MPN最大．”如图，其结论是：点P为过M，N两点且和射线QB相切的圆与射线QB的切点．根据以上结论解决以下问题：在平面直角坐标系xOy中，给定两点M（0，2），N（2，4），点P在x轴上移动，当∠MPN取最大值时，点P的横坐标是（　　）

  A．2

  B．6

  C．2或6

  D．1或3
  组卷：186引用：3难度：0.6

  解析

四、解答题（本题共6小题，共70分。解答应写出必要的文字说明、证明过程或演算步骤）

• 21．古希腊时期与欧几里得、阿基米德齐名的著名数学家阿波罗尼斯发现：平面内到两个定点的距离之比为定值λ（λ＞0且λ≠1）的点所形成的图形是圆，后人将这个圆称为阿波罗尼斯圆．已知点A（0，6）、B（0，3），动点M满足

  |

  MA

  |

  |

  MB

  |

  =

  1

  2

  ．记动点M的轨迹为曲线C．
  （1）求曲线C的方程；
  （2）过点N（0，4）的直线l与曲线C交于P，Q两点，若P为线段NQ的中点，求直线l的方程．
  组卷：30引用：2难度：0.6

  解析

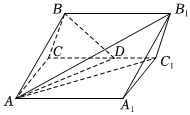• 22．如图，在三棱柱ABC-A₁B₁C₁中，底面ABC是边长为8的等边三角形，AA₁≥AB，AA₁⊥AC，∠BAA₁=60°，D在棱CC₁上且满足CD=AC．
  （1）求证：平面ACC₁A₁⊥平面BAD；
  （2）若平面ABC与平面AB₁C₁夹角的余弦值为

  3

  17

  17

  ，求三棱柱ABC-A₁B₁C₁的体积．
  组卷：14引用：1难度：0.5

  解析