当前位置：试卷中心 > 试卷详情

2023-2024学年广西南宁外国语学校九年级（上）月考数学试卷（9月份）

发布：2024/8/30 2:0:8

一、选择题（本大题共12小题，每小题3分，共36分）

1．-2的相反数是（　　）
A．2 B．-2 C．
-
1
2
D．
1
2
组卷：4766引用：1083难度：0.9
解析
2．下列图案中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：968引用：11难度：0.8
解析
3．下列运算正确的是（　　）
A．a³•a²=a⁵ B．a¹⁰÷a²=a⁵
C．a²+a²=2a⁴ D．（a+3）²=a²+9
组卷：37引用：10难度：0.9
解析
4．下列问题中应采用全面调查的是（　　）
A．检测某城市的空气质量
B．了解全国中学生的视力和用眼卫生情况
C．调查某池塘中现有鱼的数量
D．企业招聘，对应聘人员进行面试
组卷：521引用：10难度：0.8
解析
5．已知⊙O的半径为5，点P到圆心O的距离为7，那么点P与⊙O的位置关系是（　　）
A．点P在⊙O上 B．点P在⊙O内 C．点P在⊙O外 D．无法确定
组卷：376引用：19难度：0.9
解析
6．不等式组
2
x
+
2
＞
0
-
x
≥
-
1
的解集在数轴上表示为（　　）
A． B．
C． D．
组卷：947引用：38难度：0.9
解析
7．将抛物线y=2x²向上平移3个单位得到的抛物线的解析式是（　　）
A．y=2x²+3 B．y=2x²-3 C．y=2（x+3）² D．y=2（x-3）²
组卷：125引用：42难度：0.9
解析
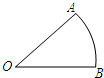8．如图，一只蚂蚁从O点出发，沿着扇形OAB的边缘匀速爬行一周，设蚂蚁的运动时间为t,蚂蚁到O点的距离为S，则S关于t的函数图象大致为（　　）
A． B． C． D．
组卷：634引用：66难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（本大题共8小题，共计72分）

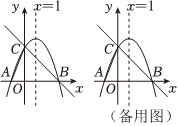25．如图，抛物线y=ax²+2x+c的对称轴是直线x=1，与x轴交于点A，B（3，0），与y轴交于点C，连接AC．
（1）求此抛物线的解析式；
（2）已知点D是第一象限内抛物线上的一个动点，过点D作DM⊥x轴，垂足为点M，DM交直线BC于点N，是否存在这样的点N，使得以A，C，N为顶点的三角形是等腰三角形．若存在，请求出点N的坐标，若不存在，请说明理由．
组卷：282引用：2难度：0.5
解析
26．【问题提出】如图1，AB为⊙O的一条弦，点C在弦AB所对的优弧上运动时，根据圆周角性质，我们知道∠ACB的度数不变．爱动脑筋的小芳猜想，如果平面内线段AB的长度已知，∠ACB的大小确定，那么点C是不是在某个确定的圆上运动呢？
【问题探究】为了解决这个问题，小芳先从一个特殊的例子开始研究．如图2，若AB=4，线段AB上方一点C满足∠ACB=45°，为了画出点C所在的圆，小芳以AB为底边构造了一个Rt△AOB，再以点O为圆心，OA为半径画圆，则点C在⊙O上．后来小芳通过逆向思维及合情推理，得出一个一般性的结论．即：若线段AB的长度已知，∠ACB的大小确定，则点C一定在某一个确定的圆上，即定弦定角必定圆，我们把这样的几何模型称之为“定弦定角”模型．
【模型应用】（1）若
AB
=
6
3
，平面内一点C满足∠ACB=60°，若点C所在圆的圆心为O，则∠AOB=
，半径OA的长为
；
（2）如图3，已知正方形ABCD以AB为腰向正方形内部作等腰△ABE，其中AB=AE，过点E作EF⊥AB于点F，若点P是△AEF的内心．
①求∠BPA的度数；
②连接CP，若正方形ABCD的边长为6，求CP的最小值．
组卷：637引用：5难度：0.4
解析