2022-2023学年山西省朔州市怀仁一中高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．集合{α|k•180°≤α≤k•180°+60°，k∈Z}中的角所表示的范围（阴影部分）是（　　）

  A．

  B．

  C．

  D．
  组卷：929引用：9难度：0.7

  解析

• 2．已知向量|

  a

  |=

  3

  ，|

  b

  |=2，它们的夹角为

  π

  6

  ，则|

  a

  +

  b

  |=（　　）

  A．10

  B． 10

  C． 13

  D．13
  组卷：310引用：12难度：0.9

  解析

• 3．在△ABC中，角A，B，C的对边分别为a,b,c,a=6，

  A

  =

  π

  3

  ，则△ABC外接圆的面积为（　　）

  A．4π

  B．12π

  C．16π

  D．48π
  组卷：514引用：13难度：0.9

  解析

• 4．函数f（x）=4sin²x-1的最小正周期是（　　）

  A．π

  B． π 2

  C． 3 π 2

  D．2π
  组卷：272引用：8难度：0.8

  解析

• 5．某圆锥的侧面积为8，用一个平行于圆锥底面的平面截该圆锥得到一个圆台，若圆台上底面和下底面半径之比为

  1

  3

  ，则该圆台的侧面积为（　　）

  A． 8 9

  B． 16 9

  C． 32 9

  D． 64 9
  组卷：58引用：2难度：0.5

  解析

• 6．从装有2个红色乒乓球和3个白色乒乓球的口袋内任取3个球，那么是互斥事件而不是对立事件的两个事件是（　　）

  A．恰有1个白色乒乓球与至少2个白色乒乓球

  B．至少2个白色乒乓球与都是白色乒乓球

  C．至少1个白色乒乓球与至少1个红色乒乓球

  D．恰有1个红色乒乓球与恰有1个白色乒乓球
  组卷：113引用：6难度：0.7

  解析

• 7．已知m,n是两条不同的直线，α，β，γ是三个不同的平面，则下列说法正确的是（　　）

  A．若α⊥β，α∩β=n,m⊥n,则m⊥β

  B．若m⊥α，n⊥β，α⊥β，则m⊥n

  C．若α⊥γ，β⊥γ，则α⊥β

  D．若α∥β，β∥γ，m⊂α，n⊂γ，则m∥n
  组卷：106引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出必要的文字说明、证明过程及演算步骤.

• 21．在△ABC中，角A，B，C的对边分别是a,b,c,且

  2

  3

  sin

  B

  =

  （

  b

  +

  c

  +

  a

  ）

  （

  b

  +

  c

  -

  a

  ）

  ac

  ．
  （1）求角A的大小；
  （2）若△ABC为锐角三角形，且bcosC+ccosB=1，求△ABC的面积的取值范围．
  组卷：43引用：3难度：0.5

  解析

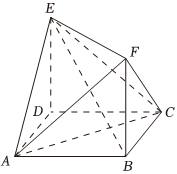• 22．如图，四边形ABCD是正方形，四边形BDEF是矩形，平面ABCD⊥平面BDEF，直线BE与平面ADE所成角的正切值为

  6

  3

  ．
  （1）求证：平面ACE⊥平面ACF；
  （2）求二面角E-AF-C的大小．
  组卷：66引用：2难度：0.5

  解析