2022-2023学年上海市金山区华东师大三附中高二（下）期末数学试卷

一、填空题（第1-6题每题4分，第7-12题每题5分，满分54分）

• 1．已知直线l：x=2y+1，则直线l的斜率k=

  ．
  组卷：84引用：4难度：0.8

  解析

• 2．已知

  P

  （

  A

  ）

  =

  1

  4

  ，

  P

  （

  A

  ∩

  B

  ）

  =

  1

  8

  ，则P（B|A）=

  ．
  组卷：92引用：3难度：0.7

  解析

• 3．函数f（x）=x在区间[2，4]上的平均变化率为

  ．
  组卷：107引用：3难度：0.9

  解析

• 4．已知双曲线C：

  y

  2

  4

  -

  x

  2

  5

  =

  1

  ，则双曲线C的离心率e=

  ．
  组卷：16引用：1难度：0.7

  解析

• 5．已知M={1，2，3}，且m∈M，n∈M，方程

  x

  2

  m

  -

  y

  2

  n

  =

  1

  表示的曲线是双曲线，则有

  条不同的双曲线．
  组卷：30引用：1难度：0.7

  解析

• 6．掷一颗骰子，则掷得点数的期望是

  ．
  组卷：38引用：1难度：0.5

  解析

• 7．已知P：1＜m＜3，Q：

  x

  2

  m

  -

  1

  +

  y

  2

  3

  -

  m

  =

  1

  表示椭圆，则P是Q的

  条件．
  组卷：220引用：1难度：0.6

  解析

三、解答题（本大题共有5题，满分0分）

• 20．已知函数

  f

  （

  x

  ）

  =

  2

  lnx

  +

  a

  x

  2

  ．
  （1）若f（x）在（1，f（1））处的切线与x轴平行，求a的值；
  （2）若y=f（x）在区间[2，3]上是严格增函数，求a的取值范围；
  （3）f（x）是否存在极值点，若存在求出极值点，若不存在，请说明理由．
  组卷：61引用：1难度：0.4

  解析

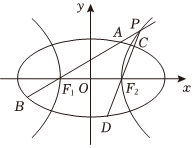• 21．如图，已知椭圆Γ₁：

  x

  2

  8

  +

  y

  2

  4

  =1的两个焦点为F₁，F₂，且F₁，F₂为双曲线Γ₂的顶点，双曲线Γ₂的离心率e=

  2

  ，设P为该双曲线Γ₂上异于顶点的任意一点，直线PF₁，PF₂的斜率分别为k₁，k₂，且直线PF₁和PF₂与椭圆Γ₁的交点分别为A，B和C，D．
  （1）求双曲线Γ₂的标准方程；
  （2）证明：直线PF₁，PF₂的斜率之积k₁•k₂为定值；
  （3）求

  |

  AB

  |

  |

  CD

  |

  的取值范围．
  组卷：107引用：6难度：0.4

  解析