2022-2023学年河南师大附中九年级(上)期中数学试卷
发布:2024/9/19 14:0:8
一、单选题(每题3分,共30分)
-
1.下列与杭州亚运会有关的图案中,中心对称图形是( )
组卷:1391引用:34难度:0.9 -
2.一元二次方程4x2-6x+1=0的二次项系数、一次项系数、常数项分别是( )
组卷:263引用:9难度:0.8 -
3.抛物线y=x2-1的顶点坐标是( )
组卷:254引用:20难度:0.9 -
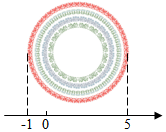 4.如图中的数轴可以度量的直径,则圆形图片的直径是( )组卷:395引用:4难度:0.6
4.如图中的数轴可以度量的直径,则圆形图片的直径是( )组卷:395引用:4难度:0.6 -
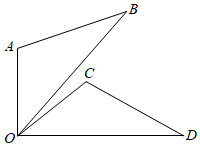 5.如图,将△AOB绕着点O顺时针旋转,得到△COD(点C落在△AOB外),若∠AOB=30°,∠BOC=10°,则最小旋转角度是( )组卷:932引用:11难度:0.7
5.如图,将△AOB绕着点O顺时针旋转,得到△COD(点C落在△AOB外),若∠AOB=30°,∠BOC=10°,则最小旋转角度是( )组卷:932引用:11难度:0.7 -
6.抛物线y=-2(x-1)2-1可由抛物线y=-2(x+2)2+3平移得到,那么平移的步骤是( )
组卷:1250引用:13难度:0.8 -
7.已知⊙O的半径为3,OA=5,则点A和⊙O的位置关系是( )
组卷:973引用:24难度:0.8
三、解答题(共75分)
-
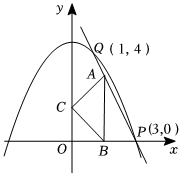 22.已知抛物线y=ax2+c(a≠0)过点P(3,0),Q(1,4).
22.已知抛物线y=ax2+c(a≠0)过点P(3,0),Q(1,4).
(1)求抛物线的解析式;
(2)点A在直线PQ上且在第一象限内,过A作AB⊥x轴于B,以AB为斜边在其左侧作等腰直角ABC.
①若A与Q重合,求C到抛物线对称轴的距离;
②若C落在抛物线上,求C的坐标.组卷:144引用:5难度:0.5 -
23.探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,∴∠1+∠3=45°.
即∠GAF=∠.
又AG=AE,AF=AF
∴△GAF≌.
∴=EF,故DE+BF=EF.
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.12
(3)问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).12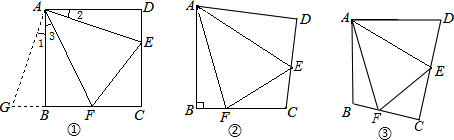 组卷:3553引用:24难度:0.1
组卷:3553引用:24难度:0.1


