2022-2023学年江苏省泰州市兴化市八年级（下）期末数学试卷

一、选择题（本大题共6小题，每小题3分，共18分，在每小题所给出的四个选项中，有一项是符合题目要求的）

• 1．下列四个高校校徽主体图案是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：40引用：3难度：0.9

  解析

• 2．下列各式中，属于最简二次根式的是（　　）

  A． 4

  B． 5

  C． 1 2

  D． 8
  组卷：79引用：2难度：0.9

  解析

• 3．⊙O半径为5，圆心O到直线l的距离为3，则直线l与⊙O的位置关系是（　　）

  A．相交

  B．相切

  C．相离

  D．无法确定
  组卷：586引用：18难度：0.9

  解析

• 4．将分式

  ab

  a

  -

  b

  中的a、b都扩大到3倍，则分式的值（　　）

  A．不变

  B．扩大3倍

  C．扩大9倍

  D．扩大6倍
  组卷：203引用：3难度：0.9

  解析

• 5．关于x的一元二次方程x²+ax-1=0的根的情况是（　　）

  A．没有实数根	B．只有一个实数根
  C．有两个相等的实数根	D．有两个不相等的实数根
  组卷：2322引用：40难度：0.7

  解析

• 6．点I是△ABC的外心，则点I是△ABC的（　　）

  A．三条垂直平分线交点	B．三条角平分线交点
  C．三条中线交点	D．三条高的交点
  组卷：580引用：6难度：0.6

  解析

二、填空题（本大题共10小题，每小题3分，共30分，请把答案直接填写在答题置上）

• 7．若分式

  2

  x

  +

  3

  无意义，则x=

  ．
  组卷：42引用：3难度：0.8

  解析

• 8．若二次根式

  5

  -

  2

  x

  在实数范围内有意义，则x的取值范围为

  ．
  组卷：148引用：5难度：0.8

  解析

三、解答题（本大题共10小题，共102分，请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

• 25．已知点M（a,a+2）（a＞0）在反比例函数

  y

  =

  k

  x

  （

  x

  ＞

  0

  ）

  的图象上，点H（0，1）在y轴上，连接MH，如图1，将MH绕着H点顺时针旋转90°至点M'，点M'正好落在x轴上．
  （1）求k的值和点M'的坐标；
  （2）若点P在反比例函数图象上，连接HP并延长至点E，使得PE=PH，连接EM'，PM'，
  ①如图2，连接MP并延长交x轴于点Q，当PM′⊥x轴时，试说明EM′平分∠PM′Q；
  ②如图3，连接MM′交HE于点Q，将△MHM'沿着MM'翻折，记点H的对应点为H'，若点H'恰好落在线段PE上，求△M′H′E与△PM′Q面积之比．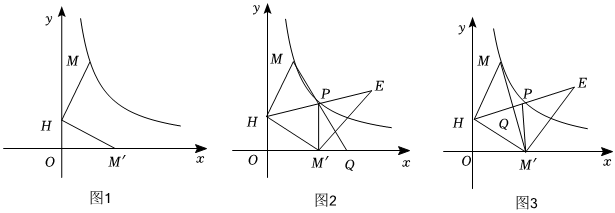
  
  组卷：759引用：4难度：0.3

  解析

• 26．已知点P（a,b）（a＞b＞0），过点P作PA⊥y轴于点A，PB⊥x轴于点B，以P为圆心，PB长为半径作圆交PA于点C，连接OC并延长交⊙P于点Q．
  （1）当点B、P、Q在同一条直线上时．
  ①如图1，点C是否为线段AP的中点？若是，请证明；若不是，请说明理由；
  ②如图2，连接OP、BC，两线交于点D，当a=4，b=2时，求CD的长；
  （2）如图3，点M为线段OC上一动点，过点M作y轴的平行线，分别交OP、AP于点N、H．若

  b

  a

  =

  m

  （m为定值），试探究在点M运动的过程中，

  MN

  AH

  的值是否为定值？如果是，请求出这个定值（用含m的代数式表示）；如果不是，请说明理由．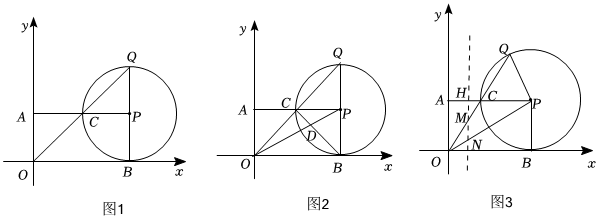
  
  组卷：71引用：1难度：0.5

  解析