当前位置：试卷中心 > 试卷详情

2023-2024学年云南省昆明八中八年级（上）期中数学试卷

发布：2024/9/28 13:0:2

1．中华文明，源远流长：中华汉字，寓意深广．下列四个选项中，是轴对称图形的为（　　）
A． B． C． D．
组卷：14引用：1难度：0.8
解析
2．下面各组线段中，不能围成三角形的是（　　）
A．3cm,4cm,5cm B．5cm,10cm,8cm
C．5cm,4.5cm,8cm D．7cm,7cm,15cm
组卷：191引用：3难度：0.5
解析
3．如图，BE⊥AC于点E，CF⊥AB于点F，若BE=CF，则Rt△BCF≌Rt△CBE的理由是（　　）
A．AAS B．HL C．SAS D．ASA
组卷：923引用：10难度：0.6
解析
4．等腰三角形的两边长分别为4cm和9cm,则这个三角形的周长为（　　）
A．22cm B．17cm或13cm C．13cm D．17cm或22cm
组卷：465引用：5难度：0.7
解析
5．计算（-4a²+12a³b）÷（-4a²）的结果是（　　）
A．1-3ab B．-3ab C．1+3ab D．-1-3ab
组卷：1814引用：8难度：0.8
解析
6．要使五边形木架（用五根木条钉成）不变形，至少要再钉上（　　）根木条．
A．1 B．2 C．3 D．4
组卷：937引用：20难度：0.9
解析
7．如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O，与AB、AC相交于点M、N，且MN∥BC．若AB=8，AC=6，BC=10，那么△AMN的周长是（　　）
A．7 B．12 C．14 D．24
组卷：507引用：4难度：0.7
解析
8．若3^x=15，3^y=5，则3^x-y等于（　　）
A．10 B．5 C．15 D．3
组卷：309引用：3难度：0.8
解析

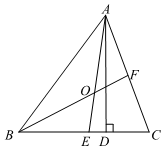23．如图，在△ABC中，AD是BC边上的高，AE、BF分别是∠BAC、∠ABC的平分线，∠BAC=56°，∠C=70°．
（1）求∠DAE的度数；
（2）求∠BOA的度数．
组卷：494引用：8难度：0.7
解析
24．八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．
【阅读理解】如图1，在△ABC中，若AB=10，BC=8，求AC边上的中线BD的取值范围．小聪同学是这样思考的：延长BD至E，使DE=BD，连接CE．利用△ABD与△CED全等将边AB转化到CE，在△BCE中利用三角形三边关系即可求出中线BD的取值范围．在这个过程中小聪同学证△ABD与△CED全等的判定方法是：
；中线BD的取值范围是
．
【阅读感悟】解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论转化到同一个三角形中．
【理解与应用】如图2，在△ABC中，∠B=90°，点D是AC的中点，点M在AB边上，点N在BC边上，若DM⊥DN．证明：AM+CN＞MN．
【问题解决】如图3，在△ABC中，点D是AC的中点，AB=MB，BC=BN，其中∠ABM=∠NBC=90°，连接MN，探索BD与MN的关系，并说明理由．
组卷：129引用：1难度：0.3
解析

A．3cm,4cm,5cm	B．5cm,10cm,8cm
C．5cm,4.5cm,8cm	D．7cm,7cm,15cm

1．中华文明，源远流长：中华汉字，寓意深广．下列四个选项中，是轴对称图形的为（ ）