2023-2024学年湖北省武汉一初慧泉中学九年级（上）月考数学试卷（10月份）

一、选择题（共10小题，每小题3分，共30分）

• 1．一元二次方程x²+2=3x的二次项系数和一次项系数分别为（　　）

  A．1，2

  B．1，3

  C．1，-2

  D．1，-3
  组卷：84引用：3难度：0.9

  解析

• 2．下面图形中既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：337引用：13难度：0.9

  解析

• 3．在下列抛物线中，其顶点是（-2，1）的是（　　）

  A．y=（x+2）2-1

  B．y=（x-2）2+1

  C．y=（x+2）2+1

  D．y=（x-2）2-1
  组卷：532引用：6难度：0.8

  解析

• 4．用配方法解一元二次方程x²+6x+2=0时，下列变形正确的是（　　）

  A．（x+3）2=9

  B．（x+3）2=7

  C．（x+3）2=3

  D．（x-3）2=7
  组卷：785引用：9难度：0.8

  解析

• 5．如图，在⊙O中，弦AB、CD相交于点P，∠A=40°，∠APD=75°，则∠B=（　　）

  A．15°

  B．35°

  C．40°

  D．75°
  组卷：767引用：6难度：0.9

  解析

• 6．将抛物线y=x²-1向上平移2个单位，再向右平移1个单位后，得到的抛物线所对应的函数表达式为（　　）

  A．y=（x-1）2-1

  B．y=（x-1）2+1

  C．y=（x+1）2+1

  D．y=（x+1）2-1
  组卷：432引用：4难度：0.6

  解析

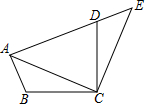• 7．如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A，D，E在同一条直线上，∠ACB=20°，则∠ADC的度数是（　　）

  A．55°

  B．60°

  C．65°

  D．70°
  组卷：8176引用：100难度：0.7

  解析

• 8．某银行经过最近两次降息，使一年期存款的年利率由2.25%降至1.98%，设平均每次降息的百分率为x,则可列方程为（　　）

  A．2×2.25%（1-x）=1.98%	B．2.25%（1-2x）=1.98%
  C．1.98%（1+x）=2.25%	D．2.25%（1-x）2=1.98%
  组卷：443引用：12难度：0.8

  解析

三、解答题（共8小题，共72分）

• 23．如图，△ABC和△CDE都是等腰直角三角形，∠BAC=∠CDE=90°，连接BD，以BD，DE为邻边作▱BDEF，连接AF，AD．
  （1）如图1，当点D落在BC上时，AD与AF的数量关系是

  ，位置关系是

  ；
  （2）如图2，当点D在△ABC的内部时，（1）中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由；
  （3）如图3，连接AE，若BC=5

  2

  ，CD=2，当BF∥AD时，直接写出AE的长．
  
  组卷：74引用：3难度：0.5

  解析

• 24．如图，已知抛物线y=-x²+2x+3与y轴交于点C，与x轴交于A、B两点（点A在点B左边）．
  （1）请直接写出A、B、C三点的坐标；
  （2）如图1，已知点M在抛物线上，点N在x轴上，且四边形AMNC为平行四边形，求M点的横坐标；
  （3）已知坐标系内有一动点F（2，n），点F不在抛物线上，直线FC交抛物线于另一点P，直线FB交抛物线交于另一点Q，连接PQ交y轴交于点G，求G点纵坐标的最大值．
  组卷：132引用：2难度：0.1

  解析