2022-2023学年贵州省黔东南州高二（下）期末数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知集合A={x|3x-1＜0}，B={0，2，4}，则A∩B=（　　）

  A．{0}

  B．{4}

  C．{0，2}

  D．{2，4}
  组卷：61引用：2难度：0.7

  解析

• 2．若cosα=-

  1

  2

  ，0＜α＜π，则tanα=（　　）

  A． 3

  B． 3 3

  C．- 3

  D．- 3 3
  组卷：217引用：4难度：0.9

  解析

• 3．已知数列{a_n}的前n项和为S_n，且满足

  S

  n

  =

  2

  n

  2

  ，则a₅=（　　）

  A．16

  B．18

  C．20

  D．25
  组卷：159引用：3难度：0.8

  解析

• 4．若iz=1+z,则z=（　　）

  A． 1 2 + 1 2 i

  B． - 1 2 + 1 2 i

  C． - 1 2 - 1 2 i

  D． 1 2 - 1 2 i
  组卷：14引用：2难度：0.8

  解析

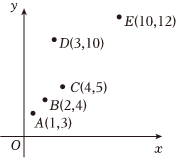• 5．根据如图所示的散点图得出的经验回归方程为

  ̂

  y

  =

  0

  .

  9

  x

  +

  ̂

  a

  ，则

  ̂

  a

  =（　　）

  A．2.8

  B．3.2

  C．3.6

  D．4
  组卷：15引用：2难度：0.7

  解析

• 6．函数f（x）的导函数为f′（x）=x²-2x,若

  f

  （

  1

  ）

  =

  1

  3

  ，则函数f（x）的极大值为（　　）

  A． - 1 3

  B．0

  C．1

  D．2
  组卷：20引用：2难度：0.5

  解析

• 7．杭州亚运会共设40个竞赛大项，包括31个奥运项目和9个非奥运项目，共设杭州赛区、宁波赛区、温州赛区、金华赛区、绍兴赛区、湖州赛区，现需从6名管理者中选取4人分别到温州，金华、绍兴、湖州四个赛区负责志愿者工作，要求四个赛区各有一名管理者，且6人中甲不去温州赛区，乙不去金华赛区，则不同的选择方案共有（　　）

  A．108种

  B．216种

  C．240种

  D．252种
  组卷：169引用：4难度：0.7

  解析

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）

• 21．已知直线l经过椭圆

  E

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右焦点F，且与椭圆E交于不同两点A，B，当直线l分别与x轴、y轴垂直时，线段AB的长分别为2、4．
  （1）求椭圆E的标准方程；
  （2）过点B作x轴的垂线交椭圆E于点C（异于点A，B），直线AC与x轴交于点D，求△ADF面积的最大值．
  组卷：39引用：3难度：0.5

  解析

• 22．已知函数f（x）=ax-lnx,a∈R．
  （1）讨论函数f（x）的单调性；
  （2）当a=1时，设

  g

  （

  x

  ）

  =

  （

  x

  -

  1

  ）

  2

  f

  （

  x

  ）

  ，求证：函数g（x）存在极大值点x₀，且

  2

  e

  2

  ＜

  g

  （

  x

  0

  ）

  ＜

  2

  3

  ．
  组卷：48引用：4难度：0.3

  解析