2022-2023学年广东省茂名一中九年级（上）期中数学试卷

一、单选题（每题3分，共30分）

• 1．下列命题中，不正确的是（　　）

  A．对角线相等的平行四边形是矩形

  B．有一个角是直角的菱形是正方形

  C．对角线相等的矩形是正方形

  D．有一组邻边相等的平行四边形是菱形
  组卷：19引用：3难度：0.6

  解析

• 2．下列四组长度的线段中，是成比例线段的是（　　）

  A．4cm,5cm,6cm,7cm	B．3cm,4cm,5cm,8cm
  C．5cm,15cm,3cm,9cm	D．8cm,4cm,1cm,3cm
  组卷：1394引用：11难度：0.8

  解析

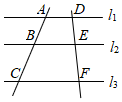• 3．如图，直线l₁∥l₂∥l₃，直线AC和DF被l₁，l₂，l₃所截，如果AB=2，BC=3，EF=2，那么DE的长是（　　）

  A．2

  B． 4 3

  C．1

  D． 3 4
  组卷：1549引用：12难度：0.6

  解析

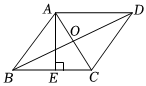• 4．如图，菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E，则AE的长是（　　）cm.

  A． 5 3

  B． 2 5

  C．9.6

  D．4.8
  组卷：25引用：3难度：0.5

  解析

• 5．某品牌服装原价为173元，连续两次降价x%后售价为127元，下面所列方程中正确的是（　　）

  A．173（1+x%）2=127	B．173（1-2x%）2=127
  C．173（1-x%）2=127	D．127（1+x%）2=173
  组卷：166引用：14难度：0.9

  解析

• 6．在一个不透明的盒子里装有若干个白球和15个红球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过多次重复试验，发现摸到白球的频率稳定在0.4左右，则袋中白球约有（　　）

  A．5个

  B．10个

  C．15个

  D．25个
  组卷：1405引用：21难度：0.9

  解析

• 7．在平面直角坐标系中，已知点A（-4，2），B（-6，-4），以原点O为位似中心，相似比为2，把△ABO放大，则点B的对应点B'的坐标是（　　）

  A．（-3，-2）	B．（-3，-2）或（3，2）
  C．（-12，-8）	D．（-12，-8）或（12，8）
  组卷：1818引用：13难度：0.6

  解析

三、解答题（16-18每题8分，19-21每题9分，22-23每题12分，共75分）

• 22．阅读材料，根据上述材料解决以下问题：
  材料1：若一元二次方程ax²+bx+c=0（a≠0）的两个根为x₁，x₂，则

  x

  1

  +

  x

  2

  =

  -

  b

  a

  ，

  x

  1

  x

  2

  =

  c

  a

  ．
  材料2：已知实数m,n满足m²-m-1=0，n²-n-1=0，且m≠n,求

  n

  m

  +

  m

  n

  的值．
  解：由题知m,n是方程x²-x-1=0的两个不相等的实数根，根据材料1得m+n=1，mn=-1，所以

  n

  m

  +

  m

  n

  =

  m

  2

  +

  n

  2

  mn

  =

  （

  m

  +

  n

  ）

  2

  -

  2

  mn

  mn

  =

  1

  +

  2

  -

  1

  =

  -

  3

  ．
  （1）材料理解：一元二次方程5x²+10x-1=0两个根为x₁，x₂，则：x₁+x₂=

  ，x₁x₂=

  ．
  （2）类比探究：已知实数m,n满足7m²-7m-1=0，7n²-7n-1=0，且m≠n,求m²n+mn²的值．
  （3）思维拓展：已知实数s、t分别满足7s²+7s+1=0，t²+7t+7=0，且st≠1．求

  2

  st

  +

  7

  s

  +

  2

  t

  的值．
  组卷：1189引用：11难度：0.5

  解析

• 23．问题背景 如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；
  尝试应用 如图（2），在△ABC和△ADE中，∠BAC=∠DAE=90°，∠ABC=∠ADE=30°，AC与DE相交于点F，点D在BC边上，

  AD

  BD

  =

  3

  ，求

  DF

  CF

  的值；
  拓展创新 如图（3），D是△ABC内一点，∠BAD=∠CBD=30°，∠BDC=90°，AB=4，AC=2

  3

  ，直接写出AD的长．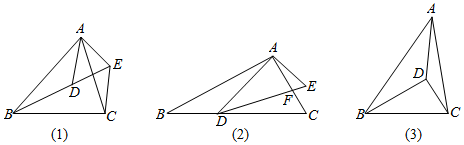
  
  组卷：11520引用：43难度：0.7

  解析