当前位置：试卷中心 > 试卷详情

2022-2023学年贵州省贵阳市高一（下）期末数学试卷

发布：2024/6/13 8:0:9

一、选择题（本大题共8小题，每小题4分，共32分。每小题有四个选项，其中只有一个选项正确，请将你认为正确的选项填写在答题卷的相应位置上.）

1．i为虚数单位，i³=（　　）
A．-i B．i C．-1 D．1
组卷：76引用：2难度：0.9
解析
2．平面直角坐标系中，已知A（1，1），B（-1，0），C（0，1），则
AB
+
AC
=（　　）
A．（-1，1） B．（-3，-1） C．（3，-1） D．（0，2）
组卷：53引用：1难度：0.8
解析
3．已知事件A，B互斥，若
P
（
A
）
=
1
5
，
P
（
A
∪
B
）
=
8
15
．则P（B）=（　　）
A．
1
3
B．
2
3
C．
7
15
D．
8
15
组卷：85引用：3难度：0.8
解析
4．已知m,n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（　　）
A．若m⊥n,n∥α，则m⊥α B．若m∥n,n⊥α，则m⊥α
C．若m⊥α，m⊥n,则n∥α D．若m⊥α，α⊥β，则m⊥β
组卷：38引用：1难度：0.5
解析
5．已知直角三角形三边长分别为3，4，5，以其中一条边所在直线为轴旋转一周后得到一个几何体，则该几何体的最大体积为（　　）
A．
48
5
π
B．12π C．16π D．32π
组卷：19引用：1难度：0.6
解析
6．从正五边形的5个顶点中任取3个构成三角形，则所得三角形是锐角三角形的概率为（　　）
A．
1
5
B．
1
3
C．
1
2
D．
2
5
组卷：20引用：1难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共4小题，每小题8分，共32分.解答应写出文字说明，证明过程或演算步骤）

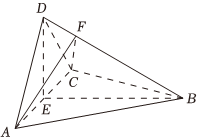19．如图，四面体A-BCD中，AD⊥CD，AD=CD，∠ADB=∠BDC，点F在BD上，E为AC的中点．
（1）证明：平面FAC⊥平面BDE；
（2）若DE⊥BE，DE=1，四面体A-BCD的体积为
3
3
，若∠AFC恰为二面角A-BD-C的平面角，求△AFC的面积．
组卷：51引用：1难度：0.6
解析

五、阅读与探究（本大题1个小题，共8分.解答应写出文字说明，条理清晰.）

20．阅读材料：
材料一：我国南宋的数学家秦九韶在《数书九章》中提出了“三斜求积术”：若把三角形的三条边分别称为小斜、中斜和大斜，记小斜为a,中斜为b,大斜为c,则三角形的面积为
S
=
1
4
[
a
2
c
2
-
（
c
2
+
a
2
-
b
2
2
）
2
]
．这个公式称之为秦九韶公式．
材料二：古希腊数学家海伦在其所著的《度量论》或称《测地术》中给出了用三角形的三条边长表示三角形的面积的公式，即已知三角形的三条边长分别为a,b,c,则它的面积为
S
=
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
，其中
p
=
1
2
（
a
+
b
+
c
）
，这个公式称之为海伦公式．
材料三：秦九韶公式和海伦公式都解决了由三角形的三边直接求三角形面积的问题．海伦公式形式优美，容易记忆，体现了数学的对称美．秦九韶公式虽然与海伦公式形式不一样，但与海伦公式完全等价，且由秦九韶在不借助余弦定理的情况下独立推出，充分说明了我国古代学者具有很高的数学水平．
材料四：印度数学家婆罗摩笈多将海伦公式推广到凸四边形（凸四边形即任取平面四边形一边所在直线，其余各边均在此直线的同侧）中，即设凸四边形的四条边长分别为a,b,c,d,
p
=
1
2
（
a
+
b
+
c
+
d
）
，凸四边形的一对对角和的半为θ，则凸四边形的面积为
S
=
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
（
p
-
d
）
-
abcdco
s
2
θ
．这个公式称之为婆罗摩笈多公式．
请你结合阅读材料解答下面的问题：
（1）在下面两个问题中选择一个作答：（如果多做，按所做的第一个问题给分）
①证明秦九韶公式与海伦公式的等价性；
②已知圆内接四边形MNPQ中，MN=2，NP=4，PQ=5，QM=3，求MNPQ的面积：
（2）△ABC中，A，B，C的对边分别为a,b,c,已知△ABC的面积为6，其内切圆半径为1，a=4，b＜c,求b,c.
组卷：72引用：2难度：0.5
解析