2022-2023学年江西省新余市高一（下）期末数学试卷

一、单项选择题（本大题有8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．

  sin

  2023

  π

  3

  的值为（　　）

  A． 1 2

  B． - 1 2

  C． 3 2

  D． - 3 2
  组卷：217引用：2难度：0.9

  解析

• 2．如图，△A′B′C′是水平放置△ABC的直观图，其中B′C′=C′A′=1，A′B′∥x′轴，A′C′∥y′轴，则BC=（　　）
  

  A． 2

  B．2

  C． 6

  D．4
  组卷：51引用：9难度：0.7

  解析

• 3．下列各式中，值为

  1

  2

  的是（　　）

  A． 2 2 （ cos 15 ° - sin 15 ° ）	B． co s 2 π 12 - si n 2 π 12
  C． tan 22 . 5 ° 1 - tan 2 22 . 5 °	D．sin15°cos15°
  组卷：138引用：6难度：0.7

  解析

• 4．函数

  f

  （

  x

  ）

  =

  sinx

  e

  x

  +

  e

  -

  x

  的部分图象可能为（　　）

  A．

  B．

  C．

  D．
  组卷：47引用：7难度：0.7

  解析

• 5．已知空间中三条不同的直线a,b,c,三个不同的平面α，β，γ，则下列说法错误的是（　　）

  A．若a∥b,a⊂α，b⊄α，则b∥α

  B．若α⊥γ，β⊥γ，则α与β平行或相交

  C．若α⊥β，a⊄α，a⊥β，则a∥α

  D．若α∩β=a,β∩γ=b,α∩γ=c,则a∥b∥c
  组卷：13引用：1难度：0.6

  解析

• 6．若

  2

  cosα

  +

  sinα

  cosα

  -

  2

  sinα

  =

  -

  1

  ，则tan2α=（　　）

  A． 4 3

  B． - 4 3

  C． - 3 4

  D． 3 4
  组卷：250引用：2难度：0.8

  解析

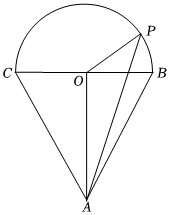• 7．如图，在△ABC中，

  AB

  =

  AC

  =

  5

  ，BC=2，以BC的中点O为圆心，BC为直径在三角形的外部作半圆弧BC，点P在半圆上运动，设∠BOP=θ，θ∈[0，π]，则

  AP

  •

  AB

  的最大值为（　　）
  

  A．5

  B．6

  C． 4 - 5

  D． 4 + 5
  组卷：37引用：1难度：0.6

  解析

四、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）

• 21．如图，四棱锥P-ABCD的侧面PAD是边长为2的正三角形，底面ABCD为正方形，且平面PAD⊥平面ABCD，Q，M，N分别为PB，AB，AD的中点．
  （1）证明：QN∥平面PDC；
  （2）证明：DM⊥PC；
  （3）求直线PM与平面PNC所成角的正弦值．​
  组卷：86引用：2难度：0.5

  解析

• 22．设函数

  f

  （

  x

  ）

  =

  sin

  （

  2

  x

  -

  π

  6

  ）

  -

  2

  si

  n

  2

  x

  +

  1

  （

  x

  ∈

  R

  ）

  ．
  （1）若

  f

  （

  α

  ）

  =

  3

  2

  ，

  α

  ∈

  [

  0

  ，

  π

  2

  ]

  ，求角α；
  （2）若不等式

  [

  f

  （

  x

  ）

  ]

  2

  +

  2

  acos

  （

  2

  x

  +

  π

  6

  ）

  -

  2

  a

  -

  2

  ＜

  0

  对任意

  x

  ∈

  （

  -

  π

  12

  ，

  π

  6

  ）

  时恒成立，求实数a的取值范围；
  （3）将函数f（x）的图像向左平移

  π

  12

  个单位，然后保持图像上点的纵坐标不变，横坐标变为原来的

  1

  m

  ，得到函数g（x）的图像，若存在非零常数λ，对任意x∈R，有g（x+λ）=λg（x）成立，求实数m的取值范围．
  组卷：30引用：1难度：0.5

  解析