当前位置：试卷中心 > 试卷详情

2021-2022学年陕西省延安一中高二（下）期中数学试卷（文科）

发布：2024/7/20 8:0:8

一、选择题：（本大题共12小题，每小题5分，满分60分。在每小题给出的四个选项中，只有一项是符合题目要求）

1．已知i是虚数单位，复数z=
3
-
i
2
+
i
在复平面中对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：32引用：2难度：0.7
解析
2．对两个变量y与x进行回归分析，分别选择不同的模型，它们的相关系数r如下，其中拟合效果最好的模型是（　　）
①模型Ⅰ的相关系数r为0.25；②模型Ⅱ的相关系数r为0.80；③模型Ⅲ的相关系数r为-0.50；④模型Ⅳ的相关系数r为-0.90．
A．Ⅰ B．Ⅱ C．Ⅲ D．Ⅳ
组卷：49引用：3难度：0.8
解析
3．“因为平行四边形的对角线互相平分，而正方形是平行四边形，所以正方形的对角线互相平分．”该推理中“正方形是平行四边形”是“三段论”的（　　）
A．大前提 B．小前提 C．结论 D．其它
组卷：2引用：1难度：0.8
解析
4．为了研究某大型超市开业天数与销售额的情况，随机抽取了5天，其开业天数与每天的销售额的情况如表所示，根据上表提供的数据，求得y关于x的线性回归方程为
̂
y
=
0
.
67
x
+
54
.
9
，请推断出数据m的值为（　　）

开业天数 10 20 30 40 50

销售额/天（万元） 62 m 75 81 89

A．68 B．68.3 C．71 D．71.3
组卷：5引用：2难度：0.7
解析
5．从2名男同学和3名女同学中任选3人参加社区服务，则选中的3人中恰有2名女同学的概率为（　　）
A．0.6 B．0.5 C．0.3 D．0.2
组卷：3引用：2难度：0.9
解析
6．用反证法证明命题：“已知a、b是自然数，若a+b≥3，则a、b中至少有一个不小于2”提出的假设应该是（　　）
A．a、b都小于2 B．a、b至少有一个不小于2
C．a、b至少有两个不小于2 D．a、b至少有一个小于2
组卷：34引用：5难度：0.9
解析
7．已知
f
（
n
）
=
1
+
1
2
+
1
3
+
⋯
+
1
n
（
n
∈
N
*
）
，计算得
f
（
2
）
=
3
2
，f（4）＞2，
f
（
8
）
＞
5
2
，f（16）＞3，
f
（
32
）
＞
7
2
，由此推测：当n≥2时，有不等式（　　）
A．
f
（
2
n
）
＞
n
+
2
2
B．
f
（
2
n
）
＞
n
+
2
2
C．
f
（
2
n
）
＞
2
n
+
1
2
D．
f
（
2
n
）
＞
2
n
+
1
2
组卷：1引用：2难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（共70分，第17题10分，第18-22题各12分。解答应写出文字说明、推理过程或演算过程。）

21．冰墩墩是2022年北京冬季奥运会的吉祥物，将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩色光环，整体形象酷似航天员，深受广大民众的喜爱，已成为最火爆的商品，“一墩难求”．某调查机构随机抽取100人，对是否有意向购买冰墩墩进行调查，结果如表：

年龄/岁 [10，20） [20，30） [30，40） [40，50） [50，60） [60，70） [70，80]

抽取人数 10 20 25 15 18 7 5

有意向购买的人数 10 18 22 9 10 4 2

（1）若从年龄在[60，70）的被调查人群中随机选出两人进行调查，求这两人中恰有一人打算购买冰墩墩的概率；
（2）若以年龄40岁为分界线，由以上统计数据完成下面的2×2列联表，并判断是否有99.9%的把握认为购买冰墩墩与人的年龄有关？

年龄低于40岁的人数年龄不低于40岁的人数总计

有意向购买冰墩墩的人数

无意向购买冰墩墩的人数

总计

参考数据：K²=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，其中n=a+b+c+d.

P（K²≥k₀） 0.15 0.10 0.05 0.025 0.010 0.005 0.001

k₀ 2.072 2.706 3.841 5.024 6.635 7.879 10.828

组卷：105引用：5难度：0.7

解析

22．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响．对近8年的年宣传费x_i和年销售量y_i（i=1，2，…，8）数据作了初步处理，
得到下面的散点图及一些统计量的值．

x

y

w

8
∑
i
=
1
（
x
i
-
x
）
2

8
∑
i
=
1
（
w
i
-
w
）
2

8
∑
i
=
1
（
x
i
-
x
）
（
y
i
-
y
）

8
∑
i
=
1
（
w
i
-
w
）
（
y
i
-
y
）

46.6 563 6.8 289.8 1.6 1469 108.8

其中w_i=
x
i
，
w
=
1
8
8
∑
i
=
1
w
i

（Ⅰ）根据散点图判断，y=a+bx与y=c+d
x
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据（Ⅱ）的结果回答下列问题：
（i）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii）年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据（u₁，v₁），（u₂，v2），…，（u_n，v_n），其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为：
̂
β
=
n
∑
i
=
1
（
u
i
-
u
）
（
v
i
-
v
）
n
∑
i
=
1
（
u
i
-
u
）
2
，
̂
α
=
v
-
̂
β
u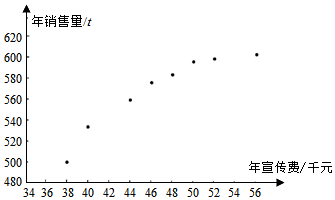
．

组卷：628引用：29难度：0.3

解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．a、b都小于2	B．a、b至少有一个不小于2
C．a、b至少有两个不小于2	D．a、b至少有一个小于2

A． f （ 2 n ）＞ n + 2 2	B． f （ 2 n ）＞ n + 2 2
C． f （ 2 n ）＞ 2 n + 1 2	D． f （ 2 n ）＞ 2 n + 1 2

年龄/岁	[10，20）	[20，30）	[30，40）	[40，50）	[50，60）	[60，70）	[70，80]
抽取人数	10	20	25	15	18	7	5
有意向购买的人数	10	18	22	9	10	4	2

	年龄低于40岁的人数	年龄不低于40岁的人数	总计
有意向购买冰墩墩的人数
无意向购买冰墩墩的人数
总计

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828

x	y	w	8 ∑ i = 1 （ x i - x ） 2	8 ∑ i = 1 （ w i - w ） 2	8 ∑ i = 1 （ x i - x ）（ y i - y ）	8 ∑ i = 1 （ w i - w ）（ y i - y ）
46.6	563	6.8	289.8	1.6	1469	108.8

开业天数	10	20	30	40	50
销售额/天（万元）	62	m	75	81	89

2021-2022学年陕西省延安一中高二（下）期中数学试卷（文科）

一、选择题：（本大题共12小题，每小题5分，满分60分。在每小题给出的四个选项中，只有一项是符合题目要求）

1．已知i是虚数单位，复数z=3-i2+i在复平面中对应的点位于（ ）

3．“因为平行四边形的对角线互相平分，而正方形是平行四边形，所以正方形的对角线互相平分．”该推理中“正方形是平行四边形”是“三段论”的（ ）

5．从2名男同学和3名女同学中任选3人参加社区服务，则选中的3人中恰有2名女同学的概率为（ ）

6．用反证法证明命题：“已知a、b是自然数，若a+b≥3，则a、b中至少有一个不小于2”提出的假设应该是（ ）

7．已知f（n）=1+12+13+⋯+1n（n∈N*），计算得f（2）=32，f（4）＞2，f（8）＞52，f（16）＞3，f（32）＞72，由此推测：当n≥2时，有不等式（ ）

三、解答题：（共70分，第17题10分，第18-22题各12分。解答应写出文字说明、推理过程或演算过程。）

1．已知i是虚数单位，复数z=
3
-
i
2
+
i
在复平面中对应的点位于（　　）

3．“因为平行四边形的对角线互相平分，而正方形是平行四边形，所以正方形的对角线互相平分．”该推理中“正方形是平行四边形”是“三段论”的（　　）

5．从2名男同学和3名女同学中任选3人参加社区服务，则选中的3人中恰有2名女同学的概率为（　　）

6．用反证法证明命题：“已知a、b是自然数，若a+b≥3，则a、b中至少有一个不小于2”提出的假设应该是（　　）

7．已知
f
（
n
）
=
1
+
1
2
+
1
3
+
⋯
+
1
n
（
n
∈
N
*
）
，计算得
f
（
2
）
=
3
2
，f（4）＞2，
f
（
8
）
＞
5
2
，f（16）＞3，
f
（
32
）
＞
7
2
，由此推测：当n≥2时，有不等式（　　）