2023-2024学年辽宁省部分重点中学协作体高二（上）期中数学模拟试卷（A卷）

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．直线x+y-1=0的倾斜角是（　　）

  A．45°

  B．60°

  C．120°

  D．135°
  组卷：148引用：4难度：0.8

  解析

• 2．无论m为何值，直线y=mx+2m+1所过定点的坐标为（　　）

  A．（-2，-1）

  B．（2，-1）

  C．（-2，1）

  D．（2，1）
  组卷：441引用：12难度：0.8

  解析

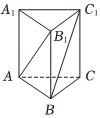• 3．如图所示，在正三棱柱ABC-A₁B₁C₁中，若

  |

  A

  B

  1

  |

  =

  3

  |

  B

  B

  1

  |

  ，则

  A

  B

  1

  与

  B

  C

  1

  的夹角为（　　）​

  A． π 4

  B． π 3

  C． π 2

  D． 2 π 3
  组卷：42引用：1难度：0.5

  解析

• 4．如图所示，已知直线l₁：y=kx+b,直线l₂：y=bx+k,则它们的图象可能为（　　）

  A．

  B．

  C．

  D．
  组卷：677引用：8难度：0.8

  解析

• 5．设入射线光线沿直线2x-y+1=0射向直线y=x,则被y=x反射后，反射光线所在的直线方程是（　　）

  A．x-2y-1=0

  B．x-2y+1=0

  C．3x-2y+1=0

  D．x+2y+3=0
  组卷：266引用：2难度：0.9

  解析

• 6．若圆（x-3）²+（y+5）²=r²上有且仅有两个点到直线4x-3y-2=0的距离为1，则半径r的取值范围是（　　）

  A．（4，6）

  B．[4，6）

  C．（4，6]

  D．[4，6]
  组卷：760引用：18难度：0.7

  解析

• 7．已知点P（x,y）在经过A（3，0）、B（1，1）两点的直线上，则2^x+4^y取最小值时点P的坐标为（　　）

  A．（-3，3）

  B．（-1，2）

  C． （ 3 2 ， 3 4 ）

  D． （ 2 ， 3 2 ）
  组卷：39引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

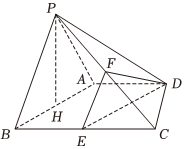• 21．如图所示，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，∠BCD=90°，E、F分别是棱BC、PC的中点，且

  AD

  =

  CD

  =

  1

  2

  BC

  =

  2

  ．
  （1）求证：DF∥平面PAB；
  （2）若点P在平面ABCD内的射影H恰为AB的中点，设PH=1，求二面角C-EF-D的余弦值．
  组卷：52引用：1难度：0.5

  解析

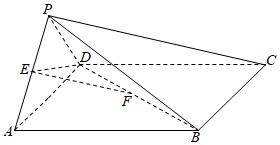• 22．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，E，F分别为PA，BD中点，PA=PD=AD=2．
  （Ⅰ）求证：EF∥平面PBC；
  （Ⅱ）求二面角E-DF-A的余弦值；
  （Ⅲ）在棱PC上是否存在一点G，使GF⊥平面EDF？若存在，指出点G的位置；若不存在，说明理由．
  组卷：464引用：11难度：0.5

  解析