2023-2024学年江西省吉安市吉安县城北中学九年级(上)月考数学试卷(10月份)
发布:2024/9/21 11:0:12
一.选择题(共6小题)
-
1.菱形具有而一般平行四边形不具有的性质是( )
组卷:1143引用:19难度:0.7 -
2.用配方法解一元二次方程x2+6x+2=0,变形后的结果正确的是( )
组卷:89引用:4难度:0.7 -
3.一个盒子中装有a个白球和3个红球(除颜色外完全相同),若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在80%左右,则a的值约为( )
组卷:418引用:10难度:0.6 -
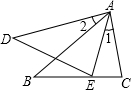 4.如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )组卷:6609引用:62难度:0.5
4.如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )组卷:6609引用:62难度:0.5 -
5.若关于x的一元二次方程ax2-2x+1=0有两个实数根,则实数a的取值范围是( )
组卷:253引用:14难度:0.9 -
 6.如图,矩形ABCD中,对角线AC,BD相交于点O,AD=2,∠COB=60°,BF⊥AC,交AC于点M,交CD于点F,延长FO交AB于点E,则下列结论:①FO=FC;②四边形EBFD是菱形;③△OBE≌△CBF;④MB=3.其中结论正确的序号是( )3组卷:679引用:10难度:0.5
6.如图,矩形ABCD中,对角线AC,BD相交于点O,AD=2,∠COB=60°,BF⊥AC,交AC于点M,交CD于点F,延长FO交AB于点E,则下列结论:①FO=FC;②四边形EBFD是菱形;③△OBE≌△CBF;④MB=3.其中结论正确的序号是( )3组卷:679引用:10难度:0.5
二.填空题(共6小题)
-
7.已知
是一元二次方程,则m=.(m-1)xm2+1+3x-5=0组卷:284引用:9难度:0.7
三.解答题(共11小题)
-
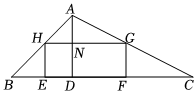 22.如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),E,F在
22.如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),E,F在
BC上,H,G分别在AB,AC上,且AD⊥BC于点D,交HG于点N.
(1)求证:△AHG∽△ABC.
(2)若AD=3,BC=9,设EH=x,则当x取何值时,矩形EFGH的面积最大?最大面积是多少?组卷:268引用:3难度:0.4 -
23.矩形ABCD中,
=ABBC(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.k2
【特例证明】
(1)如图(1),当k=2时,求证:AE=EF;
小明不完整的证明过程如下,请你帮他补充完整.
【类比探究】证明:如图,在BA上截取BH=BE,连接EH.
∵k=2,
∴AB=BC.
∵∠B=90°,BH=BE,
∴∠1=∠2=45°,
∴∠AHE=180°-∠1=135°.
∵CF平分∠DCG,∠DCG=90°,
∴∠3=∠DCG=45°.12
∴∠ECF=∠3+∠4=135°.
∴……
(只需在答题卡对应区域写出剩余证明过程)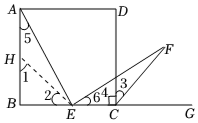
(2)如图(2),当k≠2时,求的值(用含k的式子表示);AEEF
【拓展运用】
(3)如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°,,求BC的长.PF=5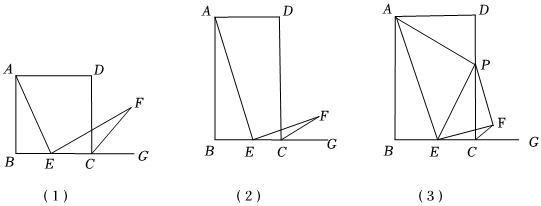 组卷:2398引用:6难度:0.2
组卷:2398引用:6难度:0.2


