2022-2023学年辽宁省鞍山市一般高中协作校高一（下）期末数学试卷

一、单选题（本大题共8个小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知z=（4+3i）（2+i），则z在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：164引用：2难度：0.8

  解析

• 2．在△ABC中，若a²+c²=b²+

  3

  ac,则角B等于（　　）

  A．120°

  B．30°

  C．45°

  D．60°
  组卷：336引用：4难度：0.7

  解析

• 3．要得到y=3sin（2x+

  π

  4

  ）的图象只需将y=3sin2x的图象（　　）

  A．向左平移 π 4 个单位	B．向右平移 π 4 个单位
  C．向左平移 π 8 个单位	D．向右平移 π 8 个单位
  组卷：769引用：131难度：0.9

  解析

• 4．在《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”，已知某“堑堵”的底面是斜边长为2的等腰直角三角形，高为2，则该“堑堵”的表面积为（　　）

  A．2 2 +2

  B．2 2 +3

  C．4 2 +4

  D．4 2 +6
  组卷：146引用：4难度：0.7

  解析

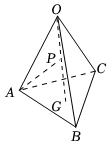• 5．如图，在四面体OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，G为△ABC的重心，P为OG的中点，则

  AP

  =（　　）

  A． - 2 3 a + 1 3 b + 1 3 c	B． 1 6 a - 1 3 b - 1 3 c
  C． - 5 6 a + 1 6 b + 1 6 c	D． 5 6 a - 1 3 b - 1 3 c
  组卷：810引用：11难度：0.8

  解析

• 6．已知平面α内有一个点A（2，-1，2），α的一个法向量为

  n

  =（3，1，2），则下列点P中，在平面α内的是（　　）

  A．（1，-1，1）

  B． （ 1 ， 3 ， 3 2 ）

  C． （ 1 ，- 3 ， 3 2 ）

  D． （ - 1 ， 3 ，- 3 2 ）
  组卷：1076引用：20难度：0.9

  解析

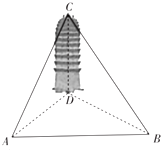• 7．如图，有一古塔，在A点测得塔底位于北偏东60°方向上的点D处，塔顶C的仰角为30°，在A的正东方向且距D点60m的B点测得塔底位于北偏西45°方向上（A，B，D在同一水平面），则塔的高度CD约为（　　）
  （参考数据：

  6

  ≈

  2

  .

  4

  ）

  A．38m

  B．44m

  C．40m

  D．48m
  组卷：140引用：7难度：0.7

  解析

四、解答题：（共6个小题，共70分。解答应写出文字说明、证明过程或演算步骤）

• 21．在边长为2的菱形ABCD中，∠BAD=60°，点E是边AB的中点（如图1），将△ADE沿DE折起到△A₁DE的位置，连接A₁B，A₁C，得到四棱锥A₁-BCDE（如图2）．
  （1）证明：平面A₁BE⊥平面BCDE；
  （2）若A₁E⊥BE，连接CE，求直线CE与平面A₁CD所成角的正弦值．
  
  组卷：678引用：6难度：0.6

  解析

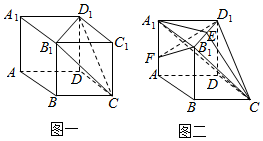• 22．如图所示，底面为菱形的直四棱柱A₁B₁C₁D₁-ABCD被过三点C、B₁、D₁的平面截去一个三棱锥C₁-CB₁D₁（图一）得几何体A₁B₁C₁D₁-ABCD（图二），E为B₁D₁的中点．
  （1）点F为棱AA₁上的动点，试问平面FB₁D₁与平面CEA₁是否垂直？请说明理由；
  （2）设AB=2，∠BAD=60°，AA₁=4，当点F为AA₁中点时，求锐二面角F-B₁D₁-C的余弦值．
  组卷：84引用：4难度：0.6

  解析