2022-2023学年黑龙江省大庆市铁人中学高二（下）期末数学试卷

一、选择题（1-8单选题，9-12多选题，部分选对得3分，全部选对得5分，共60分）

• 1．已知复数z满足z+3=4

  z

  +5i,则在复平面内复数z对应的点在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：341引用：8难度：0.8

  解析

• 2．为了了解高一、高二、高三的身体状况，现用分层抽样的方法抽出一个容量为1200的样本，三个年级学生数之比依次为k：5：3，已知高一年级共抽取了240人，则高三年级抽取的人数为（　　）

  A．240

  B．300

  C．360

  D．400
  组卷：59引用：5难度：0.9

  解析

• 3．已知15个不同数据的第25百分位数是9．则下列说法正确的是（　　）

  A．这15个数据中一定有4个数小于9

  B．把这15个数据从小到大排列后，9是第4个数据

  C．把这15个数据从小到大排列后，9是第4个数据和第5个数据的平均数

  D．把这15个数据从小到大排列后，9是第3个数据和第4个数据的平均数
  组卷：97引用：3难度：0.7

  解析

• 4．已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为（　　）

  A．30π

  B．32π

  C．37π

  D．39π
  组卷：104引用：3难度：0.7

  解析

• 5．已知平面向量

  a

  ，

  b

  满足

  a

  =（-1，2），|

  b

  |=

  10

  ，|

  a

  -

  b

  |=

  5

  ，则

  a

  与

  b

  的夹角为（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 12
  组卷：130引用：5难度：0.9

  解析

• 6．若球的最大截面圆面积扩大为原来的2倍，则球体积扩大为原来的（　　）

  A．8倍

  B．4倍

  C． 2 2 倍

  D．2倍
  组卷：11引用：2难度：0.7

  解析

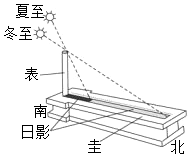• 7．圭表（圭是南北方向水平放置测定表影长度的刻板，表是与圭垂直的杆）是中国古代用来确定节令的仪器，利用正午时太阳照在表上，表在圭上的影长来确定节令．已知冬至和夏至正午时，太阳光线与地面所成角分别为α，β，表影长之差为l,那么表高为（　　）

  A． l （ tanα - tanβ ） tanαtanβ	B． ltanαtanβ tanα - tanβ
  C． l （ tanβ - tanα ） tanβtanα	D． ltanβtanα tanβ - tanα
  组卷：97引用：4难度：0.6

  解析

三、解答题（17题10分，18-22题每题12分，共70分）

• 21．在△ABC中，角A，B，C所对的边分别为a,b,c,

  m

  =

  （

  cos

  B

  ，

  1

  ）

  ，

  n

  =

  （

  cos

  C

  ，

  3

  sin

  A

  -

  cos

  A

  ）

  ，且

  m

  ∥

  n

  
  （1）求角B的大小；
  （2）若

  b

  =

  3

  ，求a+2c的最大值．
  组卷：346引用：7难度：0.5

  解析

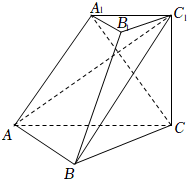• 22．在三棱台ABC-A₁B₁C₁中，AC=2，AB=

  3

  2

  ，∠BAC=60°，A₁C₁=1，CC₁=

  2

  ，AC⊥CC₁，侧面ACC₁A₁⊥平面ABC₁．
  （Ⅰ）求证：A₁C⊥平面ABC₁；
  （Ⅱ）求证：△ABC₁是直角三角形；
  （Ⅲ）求直线AA₁与平面ABC所成角的正弦值．
  组卷：259引用：3难度：0.6

  解析