2022-2023学年北京市密云区高二（下）期末数学试卷

一、选择题：本大题共10小题，每小题4分，共40分，在每小题列出的四个选项中，选出

• 1．已知集合A={-1，0，1}，B={x|x（x-1）≤0}，则A∩B=（　　）

  A．∅

  B．{0}

  C．{1}

  D．{0，1}
  组卷：144引用：5难度：0.8

  解析

• 2．已知命题p：∀x∈R，x²-2x+3＞0，则命题p的否定是（　　）

  A．∀x∈R，x2-2x+3＜0	B．∀x∈R，x2-2x+3≤0
  C．∃x∈R，x2-2x+3＜0	D．∃x∈R，x2-2x+3≤0
  组卷：214引用：6难度：0.9

  解析

• 3．已知a＞b,则下列不等式中成立的是（　　）

  A．2a＞2b

  B．ab＞b2

  C．a2＞b2

  D． 1 a ＜ 1 b
  组卷：413引用：4难度：0.8

  解析

• 4．5名同学分别报名参加学校的足球队、篮球队、乒乓球队，每人限报其中的一个运动队，不同报法的种数为（　　）

  A． C 3 5

  B． A 3 5

  C．53

  D．35
  组卷：109引用：1难度：0.9

  解析

• 5．下列函数中，在（0，+∞）上单调递增的奇函数是（　　）

  A． y = x

  B．y=x-1

  C．y=ln|x|

  D． y = x - 1 x
  组卷：227引用：1难度：0.7

  解析

• 6．某校开展“迎奥运阳光体育”活动，共设踢毽、跳绳、拔河、推火车、多人多足五个集体比赛项目，各比赛项目逐一进行．为了增强比赛的趣味性，在安排比赛顺序时，多人多足不排在第一场，拔河排在最后一场，则不同的安排方案种数为（　　）

  A．3

  B．18

  C．21

  D．24
  组卷：461引用：6难度：0.8

  解析

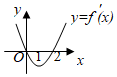• 7．设f′（x）是函数f（x）的导函数，f′（x）的图象如图所示，则f（x）的图象最有可能是（　　）

  A．

  B．

  C．

  D．
  组卷：161引用：11难度：0.9

  解析

三、解答题：本大题共6小题，共85分．解答应写出文字说明，演算步骤或证明过程．

• 20．已知函数f（x）=xe^x-ax（a∈R）．
  （Ⅰ）若y=f（x）在R上是增函数，求实数a的取值范围；
  （Ⅱ）当a=1时，判断0是否为函数f（x）的极值点，并说明理由；
  （Ⅲ）判断f（x）的零点个数，并说明理由．
  组卷：149引用：1难度：0.3

  解析

• 21．已知数列A：a₁，a₂，…，a_n，…，满足a₁=0，|a_i+1|=|a_i+1|（i=1，2，⋯，n,⋯），数列A的前n项和记为S_n．（Ⅰ）写出S₃的值；
  （Ⅱ）若a₅=-2，求S₅的值；
  （Ⅲ）是否存在数列A，使得S₂₀₂₂=1011？如果存在，写出此时a₂₀₂₃的值；如果不存在，说明理由．
  组卷：25引用：1难度：0.5

  解析