当前位置：试卷中心 > 试卷详情

2022-2023学年黑龙江省绥化市肇东四中高二（下）期中数学试卷

发布：2024/7/1 8:0:9

1．曲线y=x³-2x²在x=1处切线的斜率为（　　）
A．1 B．-1 C．7 D．-7
组卷：42引用：3难度：0.8
解析
2．从0，1，2，3，4这5个数字中选出3个不同数字能组成（　　）个三位偶数．
A．30 B．24 C．18 D．36
组卷：190引用：4难度：0.8
解析
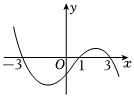3．设函数f（x）在R上可导，其导函数为f'（x），且函数f'（x）的图像如图所示，则函数f（x）的极小值为（　　）
A．f（-3） B．f（3） C．f（2） D．f（1）
组卷：42引用：2难度：0.6
解析
4．某地教育部门为了解小学生的视力状况，要从该地甲、乙、丙、丁4所小学中随机抽取2所进行检查，则甲小学被抽到的概率为（　　）
A．
1
4
B．
1
3
C．
1
2
D．
2
3
组卷：153引用：4难度：0.8
解析
5．函数f（x）=2lnx-x的单调增区间为（　　）
A．（-∞，2） B．（-2，2） C．（0，2） D．（2，+∞）
组卷：834引用：13难度：0.8
解析
6．小陈和小李是某公司的两名员工，在每个工作日小陈和小李加班的概率分别为
1
3
和
1
4
，且两人同时加班的概率为
1
6
，则某个工作日，在小李加班的条件下，小陈也加班的概率为（　　）
A．
1
12
B．
1
2
C．
2
3
D．
3
4
组卷：95引用：3难度：0.7
解析
7．二项式
（
x
-
1
x
）
10
的展开式中二项式系数最大的项为（　　）
A．第6项 B．第5、6项 C．第7项 D．第6、7项
组卷：41引用：2难度：0.7
解析

21．设某厂有甲、乙、丙三个车间生产同一种产品，已知各车间的产量分别占全厂产量的25%，35%，40%，并且各车间的次品率依次为5%，4%，2%．现从该厂这批产品中任取一件．
（1）求取到次品的概率；
（2）若取到的是次品，则此次品由三个车间生产的概率分别是多少？
组卷：296引用：10难度：0.6
解析
22．已知a∈R，函数
f
（
x
）
=
1
3
x
3
-
1
2
（a-1）x²-ax-3，g（x）=x-2lnx.
（1）当a=1时，求函数y=f（x）在点（3，f（3））处的切线方程；
（2）若函数f（x）的减区间是（-1，4），求a的值；
（3）若函数y=g（x）-a在[1，3]上恰有两个不同的零点，求实数a的取值范围．
组卷：185引用：3难度：0.4
解析