2023-2024学年天津四十七中高二（上）期中数学试卷

一、选择题（每题5分，共45分）

• 1．直线

  3

  x-3y-2m=0（m∈R）的倾斜角为（　　）

  A．120°

  B．60°

  C．30°

  D．150°
  组卷：83引用：6难度：0.8

  解析

• 2．已知直线l₁：ax+y+a=0与l₂：（a-6）x+（a-4）y-4=0，则“a=2”是“l₁∥l₂”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：184引用：7难度：0.8

  解析

• 3．已知A（2，1，3），B（2，-2，6），C（3，6，6），则

  AC

  在

  AB

  上的投影向量为（　　）

  A．（0，-1，1）

  B． （ 0 ，- 2 ， 2 ）

  C． （ 0 ， 2 ，- 2 ）

  D．（0，1，-1）
  组卷：134引用：5难度：0.8

  解析

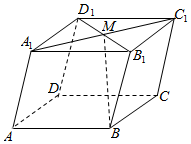• 4．如图，在平行六面体ABCD-A₁B₁C₁D₁中，M为A₁C₁，B₁D₁的交点．若

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则向量

  BM

  =（　　）

  A．- 1 2 a + 1 2 b + c

  B． 1 2 a + 1 2 b + c

  C．- 1 2 a - 1 2 b + c

  D． 1 2 a - 1 2 b + c
  组卷：1907引用：49难度：0.7

  解析

• 5．抛物线x²=16y的焦点到圆C：（x-3）²+y²=1上点的距离的最大值为（　　）

  A．6

  B．2

  C．5

  D．8
  组卷：136引用：3难度：0.7

  解析

• 6．一条沿直线传播的光线经过点P（-4，8）和Q（-3，6），然后被直线y=x-3反射，则反射光线所在的直线方程为（　　）

  A．x+2y-3=0

  B．2x+y-15=0

  C．x-2y-5=0

  D．x+2y+3=0
  组卷：200引用：6难度：0.7

  解析

三、解答题（共75分，解答需写出必要的文字说明推理过程或计算步骤，只有结果的不给分）

• 19．如图，椭圆E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）经过点A（0，-1），且离心率为

  2

  2

  ．
  （Ⅰ）求椭圆E的方程；
  （Ⅱ）经过点（1，1），且斜率为k的直线与椭圆E交于不同两点P，Q（均异于点A），问直线AP与AQ的斜率之和是否为定值，若是，求出这个定值；若不是，请说明理由．
  组卷：2097引用：20难度：0.3

  解析

• 20．已知椭圆E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的离心率为

  1

  2

  ，圆O：x²+y²=r²（r＞0）与x轴交于点M、N，P为椭圆E上的动点，|PM|+|PN|=2a,△PMN面积最大值为

  3

  ．
  （Ⅰ）求圆O与椭圆E的方程；
  （Ⅱ）圆O的切线l交椭圆E于点A、B，求|AB|的取值范围．
  组卷：432引用：4难度：0.1

  解析