2022-2023学年新疆和田地区皮山县高二（上）期中数学试卷

一、单选题（8*5=40）

• 1．双曲线

  x

  2

  4

  -

  y

  2

  5

  =

  1

  的焦距等于（　　）

  A．2

  B．4

  C．3

  D．6
  组卷：61引用：7难度：0.7

  解析

• 2．直线l₁：3x+4y-7=0与直线l₂：6x+8y+1=0间的距离为（　　）

  A． 8 5

  B． 3 2

  C．4

  D．8
  组卷：457引用：4难度：0.8

  解析

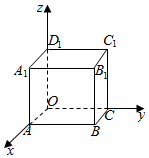• 3．在如图所示空间直角坐标系内，正方体ABCD-A₁B₁C₁D₁的棱长为1，则棱BB₁中点的坐标为（　　）

  A．（1，1， 1 2 ）

  B．（1， 1 2 ，1）

  C．（ 1 2 ，1，1）

  D．（ 1 2 ， 1 2 ， 1 ）
  组卷：220引用：3难度：0.8

  解析

• 4．当圆x²+y²=4截直线l：x-my+m-1=0（m∈R）所得的弦最长时，则m的值为（　　）

  A． - 2

  B．-1

  C．1

  D． 2
  组卷：10引用：1难度：0.8

  解析

• 5．设抛物线y²=8x上一点P到y轴的距离是4，则点P到该抛物线焦点的距离是（　　）

  A．4

  B．6

  C．8

  D．12
  组卷：1581引用：59难度：0.9

  解析

• 6．已知空间四边形ABCD的每条边和对角线的长都等于1，点E，F分别是BC，AD的中点，则

  AE

  •

  AF

  的值为（　　）

  A．1

  B． 1 2

  C． 1 4

  D． 3 4
  组卷：25引用：5难度：0.5

  解析

• 7．已知椭圆

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左右焦点分别为F₁（-c,0），F₂（c,0），若椭圆上存在点P，使PF₁=3PF₂，则该椭圆离心率的取值范围为（　　）

  A． （ 0 ， 1 2 ）

  B． （ 0 ， 1 2 ]

  C． [ 1 2 ， 1 ）

  D． （ 1 2 ， 1 ）
  组卷：60引用：1难度：0.6

  解析

四、解答题（共70分）

• 21．如图，三棱锥P-ABC中，PA，PB，PC两两垂直，PA=PB=PC，且M，N分别为线段AB，PC的中点．
  （1）若点K是线段PM的中点，求证：直线NK∥平面ABC；
  （2）求证：平面PCM⊥平面ABC．
  组卷：547引用：3难度：0.5

  解析

• 22．已知双曲线E：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的左焦点F为（-2，0），点

  M

  （

  3

  ，

  2

  ）

  是双曲线E上的一点．
  （1）求E的方程；
  （2）已知过坐标原点且斜率为k（k＞0）的直线l交E于A，B两点，连接FA交E于另一点C，连接FB交E于另一点D，若直线CD经过点N（0，-1），求直线l的斜率k.
  组卷：283引用：6难度：0.4

  解析