2022-2023学年四川省攀枝花市高二（上）期末数学试卷（文科）

一．选择题（本大题共$12$小题，每小题$5$分，总分$60$分）

• 1．对抛物线y=

  1

  4

  x²，下列描述正确的是（　　）

  A．开口向上，焦点为（0，1）

  B．开口向右，焦点为（1，0）

  C．开口向上，焦点为（0， 1 16 ）

  D．开口向右，焦点为（ 1 16 ，0）
  组卷：208引用：3难度：0.9

  解析

• 2．命题“∀x∈R，都有x²≥0”的否定为（　　）

  A．不存在x0∈R，使得 x 2 0 ＜ 0	B．∀x∈R，都有x2＜0
  C．∃x0∈R，使得 x 2 0 ≥ 0	D．∃x0∈R，使得 x 2 0 ＜ 0
  组卷：50引用：6难度：0.9

  解析

• 3．已知随机事件A和B互斥，且P（A∪B）=0.6，P（A）=0.4，则事件B的对立事件的概率为（　　）

  A．0.2

  B．0.4

  C．0.6

  D．0.8
  组卷：65引用：2难度：0.7

  解析

• 4．已知F₁，F₂是椭圆C：

  x

  2

  9

  +

  y

  2

  4

  =1的两个焦点，点M在C上，则|MF₁|•|MF₂|的最大值为（　　）

  A．13

  B．12

  C．9

  D．6
  组卷：9469引用：51难度：0.7

  解析

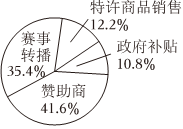• 5．2022年第24届冬奥会在北京和张家口成功举办，出色的赛事组织工作赢得了国际社会的一致称赞，经济效益方面，多项收入也创下历届冬奥会新高．某机构对本届冬奥会各项主要收入进行了统计，得到的数据如图所示．已知赛事转播的收入比政府补贴和特许商品销售的收入之和多27亿元，则估计2022年冬奥会这几项收入总和约为（　　）

  A．118亿元

  B．143亿元

  C．218亿元

  D．223亿元
  组卷：45引用：2难度：0.5

  解析

• 6．下列命题为真命题的是（　　）

  A．“∃x∈R，x2+x-2＞0”的否定

  B．“若x＞y,则x2＞y2”的否命题

  C．“若x=y,则sinx=siny”的逆命题

  D．“若x2+y2=0，则xy=0”的逆否命题
  组卷：18引用：1难度：0.8

  解析

• 7．2021年某省高考体育百米测试中，成绩全部介于12秒与18秒之间，抽取其中100个样本，将测试结果按如下方式分成六组：第一组[12，13），第二组[13，14），…，第六组[17，18]，得到如下频率分布直方图．则该100名考生的成绩的平均数和中位数（保留一位小数）分别是（　　）
  

  A．15.2  15.4

  B．15.1  15.4

  C．15.1  15.3

  D．15.2  15.3
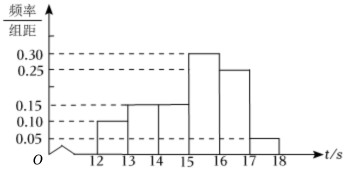  组卷：28引用：6难度：0.7

  解析

三．解答题（本大题共$6$小题，总分$70$分）

• 21．已知抛物线E：y²=2px（p＞0）的焦点为F，点M（4，m）在抛物线E上，且△OMF的面积为

  1

  2

  p

  2

  （O为坐标原点）．
  （1）求抛物线E的方程；
  （2）过点F的直线l与抛物线E交于A、B两点，Q为线段AB的中点．设△OAB的面积为S，求

  |

  FQ

  |

  S

  2

  的取值范围．
  组卷：58引用：1难度：0.3

  解析

• 22．已知过点

  P

  （

  3

  ，

  1

  2

  ）

  的曲线E的方程为

  （

  x

  -

  3

  ）

  2

  +

  y

  2

  +

  （

  x

  +

  3

  ）

  2

  +

  y

  2

  =

  2

  a

  ．
  （1）求曲线E的方程；
  （2）点Q为曲线E与y轴正半轴的交点，不过点Q且不垂直于坐标轴的直线l交曲线E于S、T两点，直线QS、QT分别与x轴交于C、D两点．若C、D的横坐标互为倒数，问直线l是否过定点？如果是，求出定点坐标；如果不是，请说明理由．​
  组卷：52引用：2难度：0.5

  解析