2022-2023学年河南省南阳市方城县高一（下）期末数学试卷

一．单选题（每题5分共40分）

• 1．计算

  4

  （

  1

  +

  i

  ）

  6

  的结果是（　　）

  A． i 4

  B． - i 4

  C． i 2

  D． - i 2
  组卷：34引用：2难度：0.7

  解析

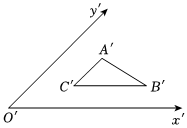• 2．如图所示是利用斜二测画法画出的水平放置的△ABC的直观图，已知A′C′∥y′轴，B′C′∥x′轴且2A′C′=B′C′=2，则△ABC的周长为（　　）

  A． 4 + 2 2

  B． 2 + 2 2

  C． 2 + 2 3

  D． 4 + 3
  组卷：134引用：5难度：0.7

  解析

• 3．sin210°cos120°的值为（　　）

  A． 1 4

  B．- 3 4

  C．- 3 2

  D． 3 4
  组卷：253引用：11难度：0.9

  解析

• 4．已知

  sin

  （

  6

  π

  5

  +

  α

  ）

  =

  3

  3

  ，则

  cos

  （

  3

  π

  5

  -

  2

  α

  ）

  =（　　）

  A． - 2 3

  B． - 1 3

  C． 2 3

  D． 1 3
  组卷：236引用：3难度：0.7

  解析

• 5．已知向量

  a

  =

  （

  λ

  +

  1

  ，

  4

  ）

  ，

  b

  =

  （

  3

  ，

  λ

  ）

  ，若

  a

  与

  b

  反向，则向量

  c

  =

  （

  1

  ，

  2

  ）

  在向量

  a

  -

  b

  上的投影向量为（　　）

  A．（6，-8）

  B．（-6，8）

  C． （ 3 5 ，- 4 5 ）

  D． （ - 3 5 ， 4 5 ）
  组卷：70引用：3难度：0.7

  解析

• 6．下列表述中正确的是（　　）

  A．若直线a∥平面α，直线b⊥a,则b⊥α

  B．若直线a⊄平面α，直线b⊂α，且 a ⊥ b ，则a⊥α

  C．若平面α内有三个不共线的点到平面β的距离相等，则α∥β

  D．若平面α，β满足α⊥β，α⊥γ，β∩γ=l,则l⊥α
  组卷：47引用：2难度：0.8

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  2

  3

  co

  s

  2

  x

  +

  （

  cosx

  -

  sinx

  ）

  2

  -

  3

  ，则（　　）

  A．f（x）的最小正周期为 π 2

  B．f（x）的一条对称轴为 x = π 6

  C．f（x）在 [ π 6 ， 2 π 3 ] 上单调递减

  D．f（x）的图象关于点 （ π 6 ， 1 ） 中心对称
  组卷：67引用：2难度：0.6

  解析

四．解答题（共70分）

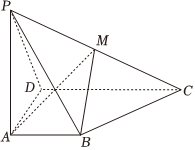• 21．如图，在四棱锥P-ABCD中，AB∥CD，AB⊥平面PAD，PA=AD=DC=2AB=4，PD=2

  7

  ，M是PC的中点．
  （1）证明：BM∥面PAD；
  （2）证明：平面ABM⊥平面PCD；
  （3）求三棱锥M-PAB的体积．
  组卷：300引用：4难度：0.5

  解析

• 22．已知函数y=f（x），若存在实数m、k（m≠0），使得对于定义域内的任意实数x,均有m•f（x）=f（x+k）+f（x-k）成立，则称函数f（x）为“可平衡”函数；有序数对（m,k）称为函数f（x）的“平衡”数对．
  （1）若f（x）=x²，求函数f（x）的“平衡”数对；
  （2）若m=1，判断f（x）=sinx是否为“可平衡”函数，并说明理由；
  （3）若m₁、m₂∈R，且

  （

  m

  1

  ，

  π

  2

  ）

  、

  （

  m

  2

  ，

  π

  4

  ）

  均为函数

  f

  （

  x

  ）

  =

  co

  s

  2

  x

  （

  0

  ＜

  x

  ≤

  π

  4

  ）

  的“平衡”数对，求

  m

  2

  1

  +

  m

  2

  2

  的取值范围．
  组卷：46引用：14难度：0.6

  解析