2022-2023学年四川省成都市锦江区嘉祥外国语高级中学高一（下）期末数学试卷

一、选择题（本题共8小题，每小题5分，共40分．每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知复数z=（k+1）i+k-1是纯虚数，则实数k=（　　）

  A．0

  B．2

  C．-1

  D．1
  组卷：44引用：1难度：0.9

  解析

• 2．已知角α的终边过点P（3，m），且

  sinα

  =

  -

  4

  5

  ，则m的值为（　　）

  A．-3

  B．3

  C．-4

  D．4
  组卷：549引用：4难度：0.7

  解析

• 3．若复数3+i为方程x²+mx+n=0（m,n∈R）的一个根，则该方程的另一个根是（　　）

  A．-3-i

  B．3-i

  C．i-3

  D．i+3
  组卷：105引用：3难度：0.7

  解析

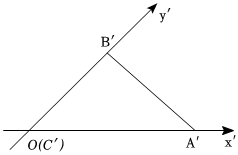• 4．已知水平放置的△ABC的直观图如图所示，A′C′=3，B'C'=2，则边AB上的中线的实际长度为（　　）

  A．5

  B． 13

  C． 5 2

  D． 13 2
  组卷：26引用：5难度：0.7

  解析

• 5．已知某圆台的高为2

  2

  ，上底面半径为1，下底面半径为2，则其侧面展开图的面积为（　　）

  A．9π

  B．6 2 π

  C．9 2 π

  D．8π
  组卷：309引用：5难度：0.8

  解析

• 6．在三棱锥P-ABC中，PA⊥底面ABC，AB=2，AC=AP，BC⊥CA，若三棱锥P-ABC外接球的表面积为5π，则BC=（　　）

  A．1

  B． 2

  C． 3

  D． 5
  组卷：224引用：9难度：0.5

  解析

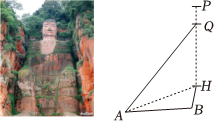• 7．位于四川省乐山市的乐山大佛，又名“凌云大佛”，是世界文化与自然双重遗产之一．如图，已知PH为佛像全身高度，PQ为佛身头部高度（PQ约为15米）．某人为测量乐山大佛的高度，选取了与佛像底部在同一水平面上的两个测量基点A，B，测得AB=40米，BH=20米，∠ABH=108°，在点A处测得点Q的仰角为48.24°，则佛像全身高度约为（　　）（参考数据：取tan48.24°=1.12，cos108°=-0.31，

  39

  =

  6

  .

  25

  ）

  A．56米

  B．69米

  C．71米

  D．73米
  组卷：80引用：7难度：0.7

  解析

四、解答题（本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）

• 21．已知锐角△ABC内角A、B、C的对边分别为a、b、c,且a（tanA+tanC）=2b•tanA．
  （1）求C的大小；
  （2）若△ABC的面积为

  3

  2

  ，求a的取值范围．
  组卷：208引用：3难度：0.6

  解析

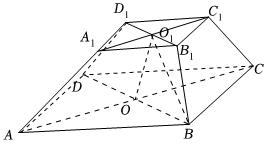• 22．如图，在四棱台ABCD-A₁B₁C₁D₁中，底面ABCD是边长为2的菱形，

  ∠

  DAB

  =

  π

  3

  ，平面BDD₁B₁⊥平面ABCD，点O₁，O分别为B₁D₁，BD的中点，O₁B=1，∠A₁AB，∠O₁BO均为锐角．
  （1）求证：AC⊥BB₁；
  （2）若异面直线CD与AA₁所成角正弦值为

  21

  7

  ，四棱锥A₁-ABCD的体积为1，求二面角B-AA₁-C的平面角的余弦值．
  组卷：320引用：6难度：0.4

  解析